题目内容
5.已知定义在R的函数$f(x)={a^x}+\frac{1}{a^x}({a>1})$.(1)判断f(x)的奇偶性和单调性,并说明理由;
(2)解关于x的不等式:f(x-1)>f(2x+1).
分析 (1)根据函数奇偶性和单调性的定义即可判断f(x)的奇偶性和单调性,并说明理由;
(2)根据函数奇偶性和单调性的性质将不等式:f(x-1)>f(2x+1)进行转化求解即可.
解答 解:(1)f(-x)=a-x+$\frac{1}{{a}^{-x}}$=ax+$\frac{1}{{a}^{x}}$=f(x),
则函数为偶函数,
当x≥0时,设0≤x1<x2,
即f(x1)-f(x2)=${a}^{{x}_{1}}$+$\frac{1}{{a}^{{x}_{1}}}$-${a}^{{x}_{2}}$-$\frac{1}{{a}^{{x}_{2}}}$=${a}^{{x}_{1}}$-${a}^{{x}_{2}}$+$\frac{1}{{a}^{{x}_{1}}}$-$\frac{1}{{a}^{{x}_{2}}}$=(${a}^{{x}_{1}}$-${a}^{{x}_{2}}$)+$\frac{{a}^{{x}_{2}}-{a}^{{x}_{1}}}{{a}^{{x}_{1}}{a}^{{x}_{2}}}$=(${a}^{{x}_{1}}$-${a}^{{x}_{2}}$)•$\frac{{a}^{{x}_{1}}{a}^{{x}_{2}}-1}{{a}^{{x}_{1}}{a}^{{x}_{2}}}$,
∵a>1,0≤x1<x2
∴1≤${a}^{{x}_{1}}$<${a}^{{x}_{2}}$,
则${a}^{{x}_{1}}$-${a}^{{x}_{2}}$<0,${a}^{{x}_{1}}$•${a}^{{x}_{2}}$-1>0,
则f(x1)-f(x2)<0,则f(x1)<f(x2),即此时函数单调递增,
同理当x≤0时,函数单调递减;
(2)∵函数f(x)是偶函数,且在[0,+∞)上为增函数,
则关于x的不等式:f(x-1)>f(2x+1)等价为f(|x-1|)>f(|2x+1|),
即|x-1|>|2x+1|,
平方得x2-2x+1>4x2+4x+1,
即3x2+6x<0,即x2+2x<0,得-2<x<0,
即不等式的解集为(-2,0).
点评 本题主要考查函数奇偶性和单调性的判断和证明,利用函数奇偶性和单调性的定义是解决本题的关键.

| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
| A. | 55 | B. | 1024 | C. | 54 | D. | 1000 |
| A. | $\frac{5}{4}<a<2$ | B. | $\frac{5}{4}≤a≤2$ | C. | $2≤a≤\frac{7}{2}$ | D. | $2<a<\frac{7}{2}$ |
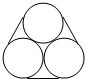 李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.
李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.