题目内容
15.已知集合A={x|a≤x≤a+4},B={x|x2-x-6≤0}.(1)当a=0时,求A∩B,A∪(∁RB);
(2)若A∪B=B,求实数a的取值范围.
分析 (1)求出B中不等式的解集确定出B,把a=0代入确定出A,找出A与B的交集,求出A与B补集的并集即可;
(2)根据A与B的并集为B,得到A为B的子集,由A与B确定出a的范围即可.
解答 解:(1)由B中不等式变形得:(x-3)(x+2)≤0,
解得:-2≤x≤3,即B={x|-2≤x≤3},
∴∁RB={x|x<-2或x>3},
把a=0代入得:A={x|0≤x≤4},
则A∩B={x|0≤x≤3},A∪(∁RB)={x|x<-2或x≥0};
(2)∵A∪B=B,∴A⊆B,
则有$\left\{\begin{array}{l}{a≥-2}\\{a+4≤3}\end{array}\right.$,
解得:-2≤a≤-1,
则实数a的范围是{a|-2≤a≤-1}.
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知等比数列{an},{bn}的公比分别为q1,q2,则q1=q2是{an+bn}为等比数列的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.抛物线${C_1}:y=\frac{1}{2p}{x^2}(p>0)$的焦点与双曲线${C_2}:\frac{x^2}{8}-{y^2}=1$的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( )
| A. | $\frac{{7\sqrt{2}}}{16}$ | B. | $\frac{{7\sqrt{2}}}{8}$ | C. | $\frac{{21\sqrt{2}}}{8}$ | D. | $\frac{{21\sqrt{2}}}{4}$ |
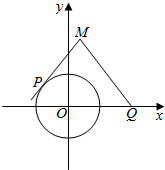 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.