题目内容
已知定义在R 上的可导函数y=f(x)满足:当x≤2时,f′(x)≤0;当x≥2时,f′(x)≥0.则下列结论:
①f′(2)=0;
②f(4)-f(3)≥0;
③f(
)-f(
)≤0;
④f(1)+f(3)≥2f(2).
其中成立的个数是( )
①f′(2)=0;
②f(4)-f(3)≥0;
③f(
| 2 |
| 3 |
| 1 |
| 3 |
④f(1)+f(3)≥2f(2).
其中成立的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:导数的运算
专题:函数的性质及应用
分析:由条件利用导数的符号可得可得函数f(x)在(-∞,2)上是减函数或常数函数、在(2,+∞)上是增函数或常数函数,由此判断各个选项是否正确,从而得出结论
解答:
解:根据当x≤2时,f′(x)≤0;当x≥2时,f′(x)≥0,
可得函数f(x)在(-∞,2)上是减函数或常数函数,在(2,+∞)上是增函数或常数函数.
故x=2是函数的极小值点,故有①f′(2)=0成立;f(4)≥f(3),故②成立;
∴f(
)≤f(
),∴③成立;
再根据f(1)≥f(2)、f(3)≥f(2),可得④f(1)+f(3)≥2f(2)成立,
故选:D.
可得函数f(x)在(-∞,2)上是减函数或常数函数,在(2,+∞)上是增函数或常数函数.
故x=2是函数的极小值点,故有①f′(2)=0成立;f(4)≥f(3),故②成立;
∴f(
| 2 |
| 3 |
| 1 |
| 3 |
再根据f(1)≥f(2)、f(3)≥f(2),可得④f(1)+f(3)≥2f(2)成立,
故选:D.
点评:本题主要考查利用导数研究函数的单调性,函数的单调性的应用,属于基础题.

练习册系列答案
相关题目
已知a、b、m为正实数,则不等式
>
成立的条件是( )
| a+m |
| b+m |
| a |
| b |
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
执行如图所示的程序框图,如果输入a=2,那么输出的a值为( )


| A、4 |
| B、16 |
| C、256 |
| D、log316 |
下列说法不正确的是( )
| A、一个命题与它的逆命题、否命题、逆否命题等四种命题中真命题个数为偶数 | ||||||||
| B、命题:“若xy=0,则x=0或y=0”的逆否命题是“若x≠0且y≠0,则xy≠0” | ||||||||
C、椭圆
| ||||||||
D、已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充分不必要条件是
|
已知i是虚数单位,(1+2i)z=i,则
=( )
. |
| z |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
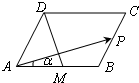 在平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,点M为AB的中点,点P从B→C→D(含端点),设∠PAB=α,记tanα=x,
在平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,点M为AB的中点,点P从B→C→D(含端点),设∠PAB=α,记tanα=x,| AP |
| DM |
A、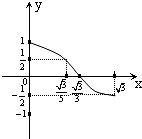 |
B、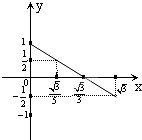 |
C、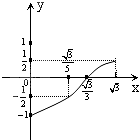 |
D、 |