题目内容
(1)①证明两角和的余弦公式
C(α+β):cos(α+β)=cos αcos β-sin αsin β;
②由C(α+β)推导两角和的正弦公式
S(α+β):sin(α+β)=sin αcos β+cos αsin β.
(2)已知cos α=-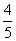 ,
,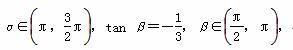 ,
,
求cos(α+β).
解析 (1)证明 ①如图,在直角坐标系xOy内作单位圆O,并作出角α,β与-β,使角α的始边为Ox轴非负半轴,交⊙O于点P1,终边交⊙O于点P2;角β的始边为OP2,终边交⊙O于点P3,角-β的始边为OP1,终边交⊙O于点P4.
则P1(1,0),P2(cos α,sin α),P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β)).
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cos α]2+[sin(-β)-sin α]2,展开并整理,得2-2cos(α+β)=2-2(cos αcos β-sin αsin β).
∴cos(α+β)=cos αcos β-sin αsin β.
 ②由①易得,cos
②由①易得,cos =sin α,
=sin α,
sin =cos α.
=cos α.
sin(α+β)=cos 
=cos
=cos cos(-β)-sin
cos(-β)-sin sin(-β)
sin(-β)
=sin αcos β+cos αsin β.
∴sin(α+β)=sin αcos β+cos αsin β.
(2)∵α∈ ,cos α=-
,cos α=-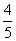 ,∴sin α=-
,∴sin α=-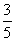 .
.
∵β∈ ,tan β=-
,tan β=- ,
,
∴cos β=- ,sin β=
,sin β= .
.
cos(α+β)=cos αcos β-sin αsin β
= ×
× -
- ×
× =
= .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
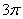 ,圆心角为
,圆心角为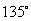 的扇形的半径为 ,面积为 .
的扇形的半径为 ,面积为 .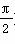 )的最小正周期是π,且f(0)=
)的最小正周期是π,且f(0)=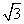 ,则( ).
,则( ).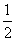 ,φ=
,φ=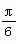 B.ω=
B.ω=
 ,sin β=
,sin β= B.
B. 
 中,角
中,角 所对边的长分别为
所对边的长分别为 ,若
,若 ,则
,则 的最小值为( )
的最小值为( ) B.
B.  C.
C. 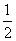 D.
D. 
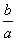 +
+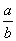 =6cos C,则
=6cos C,则 +
+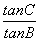 的值是________.
的值是________.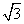 千米的C,D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.
千米的C,D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.
 则点O,N,P依次是△ABC的 ( ).
则点O,N,P依次是△ABC的 ( ).