题目内容
16.求证:sin[nπ+(-1)n•$\frac{π}{6}$]=cos[2nπ+(-1)n•$\frac{π}{3}$](n∈Z)分析 分n为奇数和偶数分别求出等式两边的值得答案.
解答 证明:当n为奇数时,左边=sin[nπ+(-1)n•$\frac{π}{6}$]=sin(nπ-$\frac{π}{6}$)=sin$\frac{π}{6}=\frac{1}{2}$,
右边=cos[2nπ+(-1)n•$\frac{π}{3}$]=cos(-$\frac{π}{3}$)=cos$\frac{π}{3}=\frac{1}{2}$,左边=右边;
当n为偶数时,左边=sin[nπ+(-1)n•$\frac{π}{6}$]=sin$\frac{π}{6}=\frac{1}{2}$,
右边=cos[2nπ+(-1)n•$\frac{π}{3}$]=cos$\frac{π}{3}=\frac{1}{2}$,左边=右边.
综上,sin[nπ+(-1)n•$\frac{π}{6}$]=cos[2nπ+(-1)n•$\frac{π}{3}$](n∈Z).
点评 本题考查三角恒等式的证明,考查了诱导公式的应用,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{\frac{3x-1}{x+3}(x≠-3)}\\{a(x=-3)}\end{array}\right.$的定义域与值域相同,则常数α=( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
13.若a为实数且$\frac{2-ai}{i}$=-2-2i,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
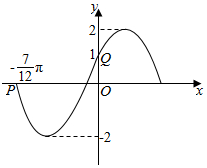 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.试确定该函数的解析式.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.试确定该函数的解析式.