题目内容
11．
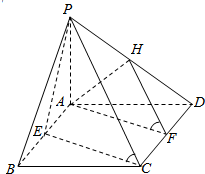如图所示，四棱锥P-ABCD的底面ABCD为矩形，PA⊥平面ABCD，PA=AD=2CD=2，E，F，H分别为AB，CD，PD的中点，求证：（1）平面AFH∥平面PCE；（2）求VD-AHF．
分析 （1）证明EC∥AF，PC∥HF，利用平面与平面平行的判定定理证明两个平面平行即可；
（2）利用等体积转换，即可得出结论．
解答 （1）证明：四棱锥P-ABCD的底面ABCD为矩形，E，F分别AB，CD的中点，
∴AE，CF平行且相等，∴四边形AECF是平行四边形，
∴EC∥AF，
∵H是PD的中点，
∴PC∥HF，
∵PC∩EC=C，AF∩HF=F，
∴平面AFH∥平面PCE．
（2）解：VD-AHF=VH-ADF=$\frac{1}{3}×\frac{1}{2}×2×\frac{1}{2}×1$=$\frac{1}{6}$．
点评 本题考查直线与平面平行，平面与平面平行的判定定理的应用，考查空间想象能力以及逻辑推理能力．
练习册系列答案
相关题目
1．执行如图所示的程序框图，则输出i的值为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
在等腰梯形ABCD中（如图），AB∥CD，DE⊥AB，AB=5，CD=3，∠DAB=$\frac{π}{3}$，现沿DE将等腰梯形折成直二面角．