题目内容
16.已知一元二次方程x2+ax+b=0的一个根在-2与-1之间,另一个根在1与2之间,画出以a,b为坐标的点(a,b)的集合表示的平面区域.分析 问题转化为二次函数f(x)=x2+ax+b与x轴的交点一个在-2与-1之间,另一个在1与2之间,结合图象可得f(-2)>0,f(-1)<0,f(1)<0,f(2)>0,写出不等式组,由线性规划的知识作图可得.
解答 解:∵一元二次方程x2+ax+b=0的一个根在-2与-1之间,另一个根在1与2之间,
∴二次函数f(x)=x2+ax+b与x轴的交点一个在-2与-1之间,另一个在1与2之间,
结合图象可得f(-2)>0,f(-1)<0,f(1)<0,f(2)>0,
∴$\left\{\begin{array}{l}{4-2a+b>0}\\{1-a+b<0}\\{1+a+b<0}\\{4+2a+b>0}\end{array}\right.$,画出以a,b为坐标的点(a,b)的集合表示的平面区域如图所示(四边形ABCD内部)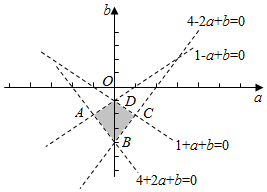
点评 本题考查一元二次方程根的分布,转化为二次函数图象与x轴的交点并数形结合是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知点P为函数f(x)=lnx的图象上任意一点,点Q为圆[x-(e+$\frac{1}{e}$)]2+y2=1任意一点,则线段PQ的长度的最小值为( )
| A. | $\frac{e-\sqrt{{e}^{2}-1}}{e}$ | B. | $\frac{\sqrt{2{e}^{2}+1}-e}{e}$ | C. | $\frac{\sqrt{{e}^{2}+1}-e}{e}$ | D. | e+$\frac{1}{e}$-1 |
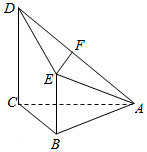 如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.
如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.