题目内容
15.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点$A(1,-\frac{{\sqrt{3}}}{2})$,直线l:y=x+m与椭圆C交于不同的两点A,B.(1)求椭圆C的方程;
(2)若△AOB的面积为1(O为坐标原点),求直线l的方程.
分析 (1)由题意可知:离心率$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,a2=4b2,将$A(1,-\frac{{\sqrt{3}}}{2})$代入椭圆方程$\frac{1}{a^2}+\frac{3}{{4{b^2}}}=1$,即可求得a和b的值,写出椭圆C的方程;
(2)将直线方程代入椭圆方程,由韦达定理,结合弦长公式即可求得丨AB丨,利用三角形的面积公式,即可求得三角形的面积公式,代入即可求得m的值,即可求得直线l的方程.
解答 解:(1)椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)焦点在x轴上,
∵离心率$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,
∴$\frac{c^2}{a^2}=\frac{3}{4}$,即$\frac{{{a^2}-{b^2}}}{a^2}=\frac{3}{4}$,得a2=4b2,①
∵椭圆C经过点$A(1,-\frac{{\sqrt{3}}}{2})$,
∴$\frac{1}{a^2}+\frac{3}{{4{b^2}}}=1$,②
联立①②,解得a2=4,b2=1,
∴椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$.
(2)设A(x1,y1),B(x2,y2),
$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得:5x2+8mx+4m2-4=0.
由△=64m2-4×5×(4m2-4)>0,解得:$-\sqrt{5}<m<\sqrt{5}$,
由韦达定理可知:${x_1}+{x_2}=-\frac{8m}{5}$,${x_1}{x_2}=\frac{{4{m^2}-4}}{5}$,
∴$|AB|=\sqrt{{1^2}+1}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$\sqrt{2}•\sqrt{{{(-\frac{8m}{5})}^2}-4•\frac{{4{m^2}-4}}{5}}=\frac{{4\sqrt{2}•\sqrt{5-{m^2}}}}{5}$,
原点O到直线l:x-y+m=0的距离$d=\frac{|m|}{{\sqrt{2}}}$,
∴${S_{△AOB}}=\frac{1}{2}|AB|•d=\frac{1}{2}•\frac{{4\sqrt{2}•\sqrt{5-{m^2}}}}{5}•\frac{|m|}{{\sqrt{2}}}=1$,
化简得,4m4-20m2+25=0,∴${m^2}=\frac{5}{2}$,
∴$m=±\frac{{\sqrt{10}}}{2}$,
∴直线l的方程为$y=x±\frac{{\sqrt{10}}}{2}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式及三角形面积公式的应用,考查计算能力,属于中档题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
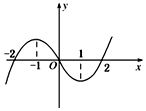 在R上可导的函数f(x)的图象如图示,f′(x)为函数f(x)的导数,则关于x的不等式x•f′(x)<0的解集为( )
在R上可导的函数f(x)的图象如图示,f′(x)为函数f(x)的导数,则关于x的不等式x•f′(x)<0的解集为( )| A. | (-∞,-1)∪(0,1) | B. | (-2,-1)∪(1,2) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-2)∪(2,+∞) |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
附:回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| A. | 50米 | B. | 75米 | C. | 100米 | D. | 125米 |
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{12}$ | D. | -$\frac{1}{12}$ |
 在底面为正三角形的三棱柱ABC-A1B1C1中,AB=2,AA1⊥平面ABC,E,F分别为BB1,AC的中点.
在底面为正三角形的三棱柱ABC-A1B1C1中,AB=2,AA1⊥平面ABC,E,F分别为BB1,AC的中点.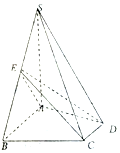 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.