题目内容
7.在150米高的山顶上,测得山下一塔的塔顶与塔底的俯角分别为30°,60°x=0,则塔高为( )| A. | 50米 | B. | 75米 | C. | 100米 | D. | 125米 |
分析 如图,设AB为山,CD为塔,Rt△ABD中利用正弦的定义,算出BD=100$\sqrt{3}$米.在△BCD中,得到∠C=120°、∠DBC=30°,利用正弦定理列式,解出CD=100米,即塔高为100米.
解答  解:如图,设AB为山,CD为塔,则
解:如图,设AB为山,CD为塔,则
Rt△ABD中,∠ADB=60°,AB=150米
∴BD=100$\sqrt{3}$米
在△BCD中,∠BDC=90°-60°=30°,∠DBC=60°-30°=30°,
∴∠C=180°-30°-30°=120°
由正弦定理,得CD=$\frac{100\sqrt{3}}{sin120°}×sin30°$=100米,即塔高为100米
故选C.
点评 本题给出实际问题,求距离山远处的一个塔的高,着重考查了直角三角形三角函数的定义和正弦定理解三角形等知识,属于基础题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
2.若直线l∥平面α,直线a?α,则l与a的位置关系是( )
| A. | l∥a | B. | l与a异面 | C. | l与a相交 | D. | l与a没有公共点 |
12.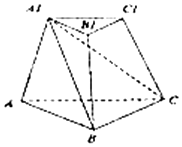 如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )
如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )
 如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )
如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 五棱锥 |
19.在等比数列{an}中,若an>0,a7=2,则$\frac{1}{a_3}+\frac{2}{{{a_{11}}}}$的最小值为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 4 | D. | 8 |
17.已知曲线y=$\frac{x^2}{4}$-lnx的一条切线的斜率为$\frac{1}{2}$,则切点的横坐标为( )
| A. | 3 | B. | 2 | C. | 2,-1 | D. | $\frac{1}{2}$ |