题目内容
若将函数f（x）=sin2x+cos2x的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是 ．
考点：函数y=Asin（ωx+φ）的图象变换,三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：把函数式f（x）=sin2x+cos2x化积为f(x)=
sin(2x+
)，然后利用三角函数的图象平移得到y=
sin（2x+
-2φ）．结合该函数为偶函数求得φ的最小正值．
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
解答：
解：由f(x)=sin2x+cos2x=
sin(2x+
)，
把该函数的图象右移φ个单位，所得图象对应的函数解析式为：
y=
sin[2(x-φ)+
]=
sin（2x+
-2φ）．
又所得图象关于y轴对称，则
-2φ=kπ+
，k∈Z．
∴当k=-1时，φ有最小正值是
．
故答案为：
．
| 2 |
| π |
| 4 |
把该函数的图象右移φ个单位，所得图象对应的函数解析式为：
y=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
又所得图象关于y轴对称，则
| π |
| 4 |
| π |
| 2 |
∴当k=-1时，φ有最小正值是
| 3π |
| 8 |
故答案为：
| 3π |
| 8 |
点评：本题考查了三角函数的图象平移，考查了三角函数奇偶性的性质，是中档题．
练习册系列答案
相关题目
函数y=
的定义域是（ ）
| 1 |
| ln(x-2) |
| A、（-∞，2） |
| B、（2，+∞） |
| C、（2，3）∪（3，+∞） |
| D、（2，4）∪（4，+∞） |
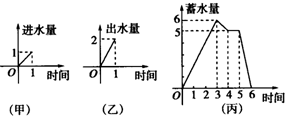水池有两个相同的进水口和一个出水口，每个口进出水速度如下图（甲）、（乙）所示，某天0点到6点该水池蓄水量如图（丙）所以（至少打开一个水口）给出以下3个论断：设0＜θ＜
，
=（sin2θ，cosθ），
=（cosθ，1），若
∥
，则tanθ=（ ）
| π |
| 2 |
| a |
| b |
| a |
| b |
A、
| ||
| B、2 | ||
| C、1 | ||
| D、0 |
已知A={x∈z|2x2+x-1=0}、B={x|4x2+1=0}．则A∪B=（ ）
A、{-
| ||||
B、{
| ||||
| C、{-1} | ||||
D、{
|