题目内容
3.已知函数$f(x)=4lnx-\frac{1}{2}m{x^2}$(m>0).(Ⅰ)若m=1,求函数f(x)的单调递增区间;
(Ⅱ)若函数g(x)=f(x)-(m-4)x,对于曲线y=g(x)上的两个不同的点M(x1,g(x1)),N(x2,g(x2)),记直线MN的斜率为k,若k=g'(x0),证明:x1+x2>2x0.
分析 (Ⅰ)当m=1,求导,令f'(x)>0,即可求得函数f(x)的单调递增区间;
(Ⅱ)g(x)=$4lnx-\frac{1}{2}m{x^2}$+(4-m)x,则g(x1)-g(x2)=4(lnx1-lnx2)$-\frac{1}{2}m({x_1^2-x_2^2})+$(4-m)(x1-x2),由题设得$g'({x_0})=\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$=$\frac{{4({ln{x_1}-ln{x_2}})}}{{{x_1}-{x_2}}}-$$\frac{1}{2}m({{x_1}+{x_2}})+({4-m})$,则$ln\frac{x_2}{x_1}-\frac{{2({\frac{x_2}{x_1}-1})}}{{\frac{x_2}{x_1}+1}}$=$lnt-\frac{{2({t-1})}}{t+1}$(t>1).构造辅助函数,求导,根据函数单调性,可知g'(x)在(0,+∞)上单调递减,则$\frac{{{x_1}+{x_2}}}{2}>{x_0}$,即x1+x2>2x0.
解答 解:(Ⅰ)依题意,当m=1时,求导$f'(x)=\frac{4}{x}-x=\frac{{4-{x^2}}}{x}$=$\frac{{({2+x})({2-x})}}{x}$.
令f'(x)>0,即2-x>0,解得0<x<2,
故函数f(x)的单调递增区间为(0,2).
(Ⅱ)依题意,g(x)=f(x)-(m-4)x=$4lnx-\frac{1}{2}m{x^2}$+(4-m)x,
g(x1)-g(x2)=4(lnx1-lnx2)$-\frac{1}{2}m({x_1^2-x_2^2})+$(4-m)(x1-x2),
=4(lnx1-lnx2)-$\frac{1}{2}m({{x_1}+{x_2}})({{x_1}-{x_2}})$+(4-m)(x1-x2).
由题设得$g'({x_0})=\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$=$\frac{{4({ln{x_1}-ln{x_2}})}}{{{x_1}-{x_2}}}-$$\frac{1}{2}m({{x_1}+{x_2}})+({4-m})$.
又$g'({\frac{{{x_1}+{x_2}}}{2}})=\frac{8}{{{x_1}+{x_2}}}-m$$•\frac{{{x_1}+{x_2}}}{2}+4-m$,
∴$g'({x_0})-g'({\frac{{{x_1}+{x_2}}}{2}})$=$\frac{{4({ln{x_1}-ln{x_2}})}}{{{x_1}-{x_2}}}-\frac{8}{{{x_1}+{x_2}}}$,
=$\frac{4}{{{x_2}-{x_1}}}[{({ln{x_2}-ln{x_1}})-\frac{{2({{x_2}-{x_1}})}}{{{x_2}+{x_1}}}}]$,
=$\frac{4}{{{x_2}-{x_1}}}[{ln\frac{x_2}{x_1}-\frac{{2({\frac{x_2}{x_1}-1})}}{{\frac{x_2}{x_1}+1}}}]$.
不妨设0<x1<x2,$t=\frac{x_2}{x_1}$,则t>1,则$ln\frac{x_2}{x_1}-\frac{{2({\frac{x_2}{x_1}-1})}}{{\frac{x_2}{x_1}+1}}$=$lnt-\frac{{2({t-1})}}{t+1}$(t>1).
令$h(t)=lnt-\frac{{2({t-1})}}{t+1}$(t>1),则$h'(t)=\frac{{{{({t-1})}^2}}}{{t{{({t+1})}^2}}}>0$,
∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,故$ln\frac{x_2}{x_1}-\frac{{2({\frac{x_2}{x_1}-1})}}{{\frac{x_2}{x_1}+1}}>0$.
又因为x2-x1>0,因此$g'({x_0})-g'({\frac{{{x_1}+{x_2}}}{2}})>0$,即$g'({\frac{{{x_1}+{x_2}}}{2}})<g'({x_0})$.
又由$g'(x)=\frac{4}{x}-mx+({4-m})$知g'(x)在(0,+∞)上单调递减,
∴$\frac{{{x_1}+{x_2}}}{2}>{x_0}$,即x1+x2>2x0.
点评 本题考查导数的综合应用,考查利用导数与函数单调性极值与最值的关系,考查学生分析问题及解决问题的能力,考查构造法,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案
| A. | m>7? | B. | m≥7? | C. | m>8? | D. | m>9? |
| A. | a>b⇒c-a<c-b | B. | $\frac{c}{a}>\frac{c}{b},c>0⇒a<b$ | C. | $a>b>0,c>d⇒\sqrt{\frac{a}{d}}>\sqrt{\frac{b}{c}}$ | D. | $\root{n}{a}<\root{n}{b}(n∈{N^*})⇒a<b$ |
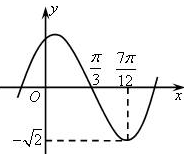 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).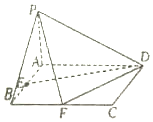 已知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=4,AB=2,E,F分别是线段AB,BC的中点.
已知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=4,AB=2,E,F分别是线段AB,BC的中点.