题目内容
设集合A={x|y=log2(-x2-2x+8)},B={y|y=x+
-2},集合C={x|(ax-
)(x+4)≤0}.
(1)求A∩B;
(2)若C⊆∁RA,求实数a的取值范围.
| 1 |
| x-1 |
| 1 |
| a |
(1)求A∩B;
(2)若C⊆∁RA,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:函数的性质及应用,集合
分析:(1)根据对数函数的真数大于0,可求得A,根据对勾函数的值域可求出B,进而可得A∩B;
(2)由(1)求出∁RA,再由C⊆∁RA,构造关于a的不等式,进而得到实数a的取值范围.
(2)由(1)求出∁RA,再由C⊆∁RA,构造关于a的不等式,进而得到实数a的取值范围.
解答:
解:(1)A={x|y=log2(-x2-2x+8)}={x|(-x2-2x+8)>0}={x|(-x+2)(x+4)>0}=(-4,2),
B={y|y=x+
-2}=B={y|y=x-1+
-1},
∵x-1+
∈(-∞,-2]∪[2,+∞),
∴B=(-∞,-3]∪[1,+∞),
∴A∩B=(-4,-3]∪[1,2)…(7分)
(2)∁RA=(-∞,-4]∪[2,+∞),
解(ax-
)(x+4)=0得:
x=
,或a=-4,
当a>0时,C=[-4,
],
又此时不满足条件C⊆∁RA,
当a<0时,C=(-∞,-4]∪[
,+∞),
又C⊆∁RA,
∴
≥2⇒a2≤
⇒-
≤a<0…(14分)
B={y|y=x+
| 1 |
| x-1 |
| 1 |
| x-1 |
∵x-1+
| 1 |
| x-1 |
∴B=(-∞,-3]∪[1,+∞),
∴A∩B=(-4,-3]∪[1,2)…(7分)
(2)∁RA=(-∞,-4]∪[2,+∞),
解(ax-
| 1 |
| a |
x=
| 1 |
| a2 |
当a>0时,C=[-4,
| 1 |
| a2 |
又此时不满足条件C⊆∁RA,
当a<0时,C=(-∞,-4]∪[
| 1 |
| a2 |
又C⊆∁RA,
∴
| 1 |
| a2 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查的知识点是集合的交并补运算,是集合运算,函数定义域和值域的综合考查,难度中档.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
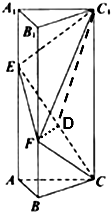 如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3
如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3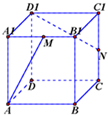 如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角
如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角