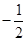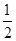题目内容
已知等比数列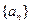 的公比为q,记
的公比为q,记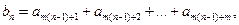
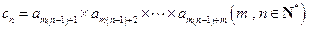 ,则以下结论一定正确的是( )
,则以下结论一定正确的是( )
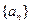 的公比为q,记
的公比为q,记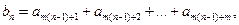
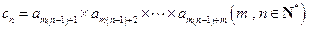 ,则以下结论一定正确的是( )
,则以下结论一定正确的是( )A.数列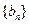 为等差数列,公差为 为等差数列,公差为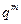 | B.数列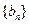 为等比数列,公比为 为等比数列,公比为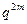 |
C.数列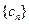 为等比数列,公比为 为等比数列,公比为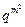 | D.数列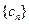 为等比数列,公比为 为等比数列,公比为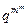 |
C
取n=1,n=2,m=3,则
b1=a1+a2+a3,b2=a4+a5+a6,c1= a1·a2·a3, c2=a4·a5·a6,
∵数列{an}是公比为q的等比数列
∴b1=a1+a2+a3= ,b2=a4+a5+a6=
,b2=a4+a5+a6=
c1= a1·a2·a3= q5, c2=a4·a5·a6=
q5, c2=a4·a5·a6= q12=
q12= q21
q21
∴ =q3,
=q3,  =q16
=q16
∴数列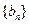 是公比为q3的等比数列,数列
是公比为q3的等比数列,数列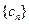 是公比为
是公比为 的等比数列
的等比数列
故选C.
b1=a1+a2+a3,b2=a4+a5+a6,c1= a1·a2·a3, c2=a4·a5·a6,
∵数列{an}是公比为q的等比数列
∴b1=a1+a2+a3=
 ,b2=a4+a5+a6=
,b2=a4+a5+a6=
c1= a1·a2·a3=
 q5, c2=a4·a5·a6=
q5, c2=a4·a5·a6= q12=
q12= q21
q21∴
 =q3,
=q3,  =q16
=q16∴数列
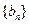 是公比为q3的等比数列,数列
是公比为q3的等比数列,数列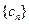 是公比为
是公比为 的等比数列
的等比数列故选C.

练习册系列答案
相关题目
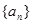 的前
的前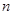 项和为
项和为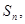 满足
满足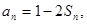 (
( 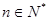 )
)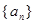 为等比数列;
为等比数列;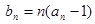 ,求数列
,求数列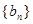 的前
的前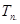
 前n项和为
前n项和为 ,首项为
,首项为 ,且
,且 等差数列。
等差数列。 ,设
,设 ,求数列
,求数列 的前n项和
的前n项和 .
. }的前n项和是
}的前n项和是 ,S5=2,S10=6,则a16+a17+a18+a19+a20等于( )
,S5=2,S10=6,则a16+a17+a18+a19+a20等于( )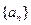 的前n项和为
的前n项和为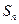 ,若
,若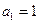 ,
,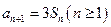 ,则
,则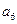 =( )
=( )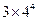
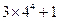
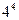
 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )



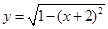 图像上存在不同的三点到原点的距离构成等比数列,则以下
图像上存在不同的三点到原点的距离构成等比数列,则以下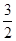
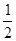
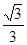
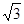
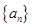 中,
中,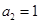 ,
,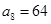 ,则
,则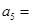 ( )
( )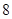
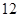
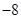
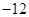
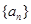 满足:
满足: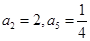 ,则公比q为( )
,则公比q为( )