题目内容
12．已知f（2x）=x+3，若f（a）=5，则a=4．分析 令a=2x，则f（a）=x+3=5，从而得出x的值，进而得出a的值．
解答 解：令a=2x，则f（a）=f（2x）=x+3=5，
∴x=2，
∴a=22=4．
故答案为4．
点评 本题考查了函数值的计算，属于基础题．
练习册系列答案
相关题目
2．设正数x，y满足log${\;}_{\frac{1}{3}}$x+log3y=m（m∈[-1，1]），若不等式3ax2-18xy+（2a+3）y2≥（x-y）2有解，则实数a的取值范围是（ ）
| A． | （1，$\frac{55}{29}$] | B． | （1，$\frac{31}{21}$] | C． | [$\frac{31}{21}$，+∞） | D． | [$\frac{55}{29}$，+∞） |
3．对?x∈（0，$\frac{1}{3}$），8x≤logax+1恒成立，则实数a的取值范围是（ ）
| A． | （0，$\frac{2}{3}$） | B． | （0，$\frac{1}{2}$] | C． | [$\frac{1}{3}$，1） | D． | [$\frac{1}{2}$，1） |
17．已知向量$\overline{a}$，$\overline{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=8，|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=4，则|2$\overrightarrow{a}$-$\overrightarrow{b}$|等于（ ）
| A． | 5 | B． | $\sqrt{5}$ | C． | 2$\sqrt{5}$ | D． | 6 |
4．已知数列{an}满足：对于?m，n∈N*，都有an•am=an+m，且${a_1}=\frac{1}{2}$，那么a5=（ ）
| A． | $\frac{1}{32}$ | B． | $\frac{1}{16}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
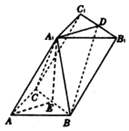如图，在三棱柱ABC-A1B1C1中，D，E分别是B1C1、BC的中点，∠BAC=90°，AB=AC=2，A1A=4，A1E=$\sqrt{14}$．