题目内容
20.函数f(x)=$\frac{{e}^{x}}{x}$的图象大致为( )| A. |  | B. |  | ||
| C. |  | D. |  |
分析 利用函数的导数判断函数的单调性以及函数的值域,判断函数的图象即可.
解答 解:函数f(x)=$\frac{{e}^{x}}{x}$的定义域为:x≠0,x∈R,当x>0时,函数f′(x)=$\frac{x{e}^{x}-{e}^{x}}{{x}^{2}}$,可得函数的极值点为:x=1,当x∈(0,1)时,函数是减函数,x>1时,函数是增函数,并且f(x)>0,选项B、D满足题意.
当x<0时,函数f(x)=$\frac{{e}^{x}}{x}$<0,选项D不正确,选项B正确.
故选:B.
点评 本题考查函数的导数的应用,判断函数的单调性以及函数的图象的判断,考查计算能力.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
10.已知向量$\overrightarrow a$,$\overrightarrow b$夹角为$\frac{π}{3}$,|$\overrightarrow b$|=2,对任意x∈R,有|$\overrightarrow b$+x$\overrightarrow a$|≥|$\overrightarrow a$-$\overrightarrow b$|,则|t$\overrightarrow b$-$\overrightarrow a$|+|t$\overrightarrow b$-$\frac{\overrightarrow a}{2}$|(t∈R)的最小值是( )
| A. | $\frac{{\sqrt{13}}}{2}$ | B. | $\frac{3}{2}$ | C. | $1+\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
8.设a,b均为实数,则“a>b”是“a3>b3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知复数z=1+2i,则z•$\overline{z}$=( )
| A. | 3-4i | B. | 5+4i | C. | -3 | D. | 5 |
5.设集合A={x|x2-16>0},B={x|-2<x≤6},则A∩B等于( )
| A. | (-2,4) | B. | (4,6] | C. | (-4,6) | D. | (-4,-2) |
10.将函数$y=2sin(\frac{2}{3}x+\frac{3π}{4})$图象上所有点的横坐标缩短为原来的$\frac{1}{3}$,纵坐标不变,再向右平移$\frac{π}{8}$个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
| A. | 函数g(x)的一条对称轴是$x=\frac{π}{4}$ | B. | 函数g(x)的一个对称中心是$(\frac{π}{2},0)$ | ||
| C. | 函数g(x)的一条对称轴是$x=\frac{π}{2}$ | D. | 函数g(x)的一个对称中心是$(\frac{π}{8},0)$ |
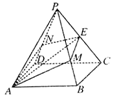 如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.
如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.