题目内容
4.已知数列{an}满足:对于?m,n∈N*,都有an•am=an+m,且${a_1}=\frac{1}{2}$,那么a5=( )| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 数列{an}对任意的m,n∈N*满足an•am=an+m,且${a_1}=\frac{1}{2}$,可得a2,a3,a4,a5.即可.
解答 解:∵数列{an}满足:对于?m,n∈N*,都有an•am=an+m,且${a_1}=\frac{1}{2}$,
∴a2=a1a1=$\frac{1}{4}$,
a3=a1•a2=$\frac{1}{8}$.
那么a4=a2•a2=$\frac{1}{16}$.
a5=a3•a2=$\frac{1}{32}$.
故选:A.
点评 本题考查了数列递推关系式的应用,考查计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知复数z=1+2i,则z•$\overline{z}$=( )
| A. | 3-4i | B. | 5+4i | C. | -3 | D. | 5 |
19.设ω>0,函数y=2cos(ωx+$\frac{π}{5}$)-1的图象向右平移$\frac{5π}{4}$个单位后与原图象重合,则ω的最小值是( )
| A. | $\frac{8}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
16.已知复数z=1+2i,则$z•\overline z$=( )
| A. | 5 | B. | 5+4i | C. | -3 | D. | 3-4i |
13.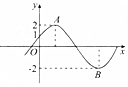 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(φx+ω)图象的对称轴为( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(φx+ω)图象的对称轴为( )
 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(φx+ω)图象的对称轴为( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(φx+ω)图象的对称轴为( )| A. | x=12k-8(k∈Z) | B. | x=6k-2(k∈Z) | C. | x=6k-4(k∈Z) | D. | x=12k-2(k∈Z) |