题目内容

7．若向量$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（3-x，2），$\overrightarrow{c}$=（4，x）满足（6$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{c}$=8，则x等于（　　）
A．4B．5C．6D．7

分析 先计算6$\overrightarrow{a}$-$\overrightarrow{b}$的坐标，再根据6$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{c}$=8列方程解出x．

解答 解：6$\overrightarrow{a}-\overrightarrow{b}$=（9+x，-8），
∴（6$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{c}$=4（9+x）-8x=36-4x=8，
∴x=7．
故选D．

点评 本题考查了平面向量的坐标运算，数量积运算，属于基础题．

练习册系列答案
相关题目
17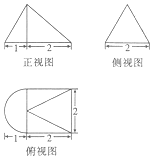．某几何体的三视图如图所示，且其侧视图是一个等边三角形，则这个几何体的表面积为（　　）
A．$\frac{（8+π）\sqrt{3}}{2}$B．$\frac{（8+π）\sqrt{3}}{6}$C．$\frac{π}{2}$+4+$\frac{5}{2}$$\sqrt{3}$D．$\frac{3}{2}$π+8+$\sqrt{7}$
18．在△ABC中，|$\overrightarrow{AB}$|=4，|$\overrightarrow{AC}$|=3，∠A=120°，D为BC边的中点，则|$\overrightarrow{AD}$|=$\frac{\sqrt{13}}{2}$．
15．已知复数z=1+2i，则z•$\overline{z}$=（　　）
A．3-4iB．5+4iC．-3D．5
2．已知点P（$\sqrt{3}$，1），Q（cosx，sinx），O为坐标原点，函数f（x）=$\overrightarrow{OP}$•$\overrightarrow{QP}$．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）若A为△ABC的内角，f（A）=4，BC=3，△ABC的面积为$\frac{3\sqrt{3}}{4}$，求△ABC的周长．
12．已知f（2x）=x+3，若f（a）=5，则a=4．
19．设ω＞0，函数y=2cos（ωx+$\frac{π}{5}$）-1的图象向右平移$\frac{5π}{4}$个单位后与原图象重合，则ω的最小值是（　　）
A．$\frac{8}{5}$B．$\frac{6}{5}$C．$\frac{4}{5}$D．$\frac{2}{5}$
16．已知复数z=1+2i，则$z•\overline z$=（　　）
A．5B．5+4iC．-3D．3-4i
17．设函数f（x）=x2+aln（x+1），a∈R．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）若函数f（x）有两个极值点x1，x2，且x1＜x2，求证：f（x2）≥（$\frac{2}{\sqrt{e}}$-1）x2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网