题目内容
在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为( ,
, ),半径r=
),半径r= ,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
(1)求圆C的直角坐标方程;
(2)求|PA||PB|的值.
(1) ;(2)|PA||PB|=|PD|2=8.
;(2)|PA||PB|=|PD|2=8.
【解析】
试题分析:(1)利用 求出圆心在直角坐标系下的坐标,写出其标准方程;
求出圆心在直角坐标系下的坐标,写出其标准方程;
(2)设圆的过点C的切线与圆相切于点D,根据切割线定理,只要求出切线CD长即可.
试题解析:【解析】
(1)圆C的圆心的极坐标为C( ,
, ),
),
∴x= =1,y=
=1,y= =1,
=1,
∴圆C的直角坐标方程为(x﹣1)2+(y﹣1)2=2.
(2)点P的极坐标为(2,π),化为直角坐标P(﹣2,0).
当直线l与圆C相切于点D时,则|PD|2=|PC|2﹣r2=(﹣2﹣1)2+(0﹣1)2﹣ =8.
=8.
∴|PA||PB|=|PD|2=8.
考点:1、极坐标与参数方程;2、直线与圆的位置关系.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
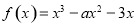
 在区间[1,+∞)上是增函数,求实数a的取值范围;
在区间[1,+∞)上是增函数,求实数a的取值范围;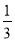 是
是 的极值点,求
的极值点,求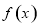 在[1,a]上的最大值;
在[1,a]上的最大值;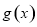 =bx的图象与函数
=bx的图象与函数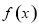 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由. 内任取一点,取到函数
内任取一点,取到函数 的图象与
的图象与 轴正半轴之间(阴影部分)的点的概率等于( )
轴正半轴之间(阴影部分)的点的概率等于( )
 B.
B.
 D.
D.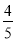
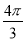 的球与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
的球与棱柱的所有面均相切,那么这个三棱柱的表面积是( )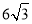 B.
B.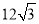 C.
C. D.
D.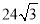
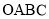 内任取一点,取到函数
内任取一点,取到函数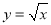 的图象与
的图象与 轴正半轴之间(阴影部分)的点的概率等于( )
轴正半轴之间(阴影部分)的点的概率等于( )
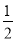 B.
B.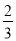
 D.
D.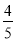
 AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.
AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.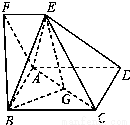
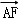 =3
=3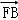 ,则弦AB的中点到准线的距离为( )
,则弦AB的中点到准线的距离为( )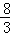 B.
B.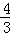 C.2 D.1
C.2 D.1
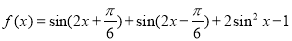 .
.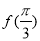 的值;
的值;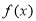 的最小正周期和单调增区间;
的最小正周期和单调增区间; 的图像是如何由函数
的图像是如何由函数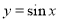 的图像变换所得.
的图像变换所得.