题目内容
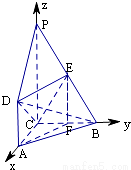
(12分)如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.

(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求二面角E﹣CD﹣B的余弦值.
(Ⅰ)详见解析;(Ⅱ)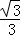 .
.
【解析】
试题分析:(Ⅰ)取BC的中点F,连结EF,AF,要证DE∥平面ABC,只要证DE∥AF,即只要证四边形ADEF是平行四边形即可;
(Ⅱ)分别以CA,CB,CP所在的直线分别为x轴,y轴,z轴,建立空间坐标系如图,根据题设写出相关点的坐标,并利用向量的坐标运算求出平面ECD和平面BCD的法向量,进而利用向的夹角公式求解.
试题解析:【解析】
(1)取BC的中点F,连结EF,
则EF∥PC∥DA,且EF= PC=DA=1,
PC=DA=1,
则四边形ADEF是平行四边形,
即DE∥AF,
∵DE平面ABC,AF平面ABC,
∴DE∥平面ABC;
(2)∵DA⊥平面ABC,DA∥PC,
∴PC⊥平面ABC,
∵∠ACB=90°,AC=AD=BC=1,PC=2,
∴分别以CA,CB,CP所在的直线分别为x轴,y轴,z轴,建立空间坐标系如图,
则A(1,0,0),B(0,1,0),D(1,0,1),P(0,0,2),
则E(0, ,1),则
,1),则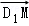 =(1,0,﹣1),
=(1,0,﹣1),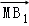 =(1,2,1),
=(1,2,1),
设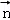 =(x,y,z)是平面ECD的法向量,
=(x,y,z)是平面ECD的法向量,
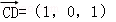 ,
,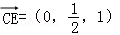 ,
,
则 ,
,
令z=1,则x=﹣1,y=﹣2,则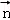 =(﹣1,﹣2,1),
=(﹣1,﹣2,1),
设 =(x,y,z)是平面BCD的法向量,
=(x,y,z)是平面BCD的法向量,
∵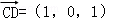 ,
, ,
,
∴ ,
,
令z=1,则x=﹣1,则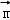 =(﹣1,0,1),
=(﹣1,0,1),
∴cos< >=
>=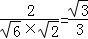 .
.
易知二面角E﹣CD﹣B为锐角,
故二面角E﹣CD﹣B的余弦值为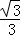 .
.
考点:1、空间直线与平面的位置关系;2、空间向量法在解决立体几何问题中的应用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 中,
中, ,则
,则 .
. ,
, ),半径r=
),半径r=
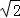 ,
, ),半径r=
),半径r=
 对任意
对任意 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 =( )
=( ) C.
C. D.
D.
 ,
, 是
是 的导函数,即
的导函数,即 ,
, ,…,
,…, ,
, ,则
,则
 B.
B.
 D.
D.