题目内容
(12分)如图,四边形ABCD为矩形,四边形ADEF为梯形,FE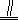
 AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.
AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.
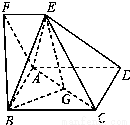
(Ⅰ)求证:EG∥平面ABF;
(Ⅱ)求三棱锥B﹣AEG的体积.
(Ⅰ)详见解析;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)取AB的中点M,连FM,GM,要证EG∥平面ABF,只要证EG∥FM,可从证明四边形GMFE为平行四边形入手;
(Ⅱ)因为 ,在平面ADEF内作EN⊥AD,垂足为N,可以证明EN⊥面ABCD,即EN为三棱锥E﹣ABG的高,再根据题设求出EN及三角形ABG的面积即可.
,在平面ADEF内作EN⊥AD,垂足为N,可以证明EN⊥面ABCD,即EN为三棱锥E﹣ABG的高,再根据题设求出EN及三角形ABG的面积即可.
试题解析:(Ⅰ)证明:取AB的中点M,连FM,GM,
∵G为对角线AC的中点,
∴GM∥AD,且GM= AD,
AD,
∵EF∥AD,

∴MG∥EF,且EF=GM,
∴四边形GMFE为平行四边形,
∴EG∥FM,
∴EG∥平面ABF.
(Ⅱ)作EN⊥AD,垂足为N,
由平面ABCD⊥面AEFD,面ABCD∩面AEFD=AD,
∴EN⊥面ABCD,即EN为三棱锥E﹣ABG的高,
∵在△AEF中,AF=FB,∠AFE=60°,
∴△AEF是正三角形,
∴∠AEF=60°,
由EF∥AD,知∠EAD=60°,
∴EN=AEsin60°= ,
,
MG= AD=EF=2,
AD=EF=2,
∴S△ABG= ×2×2=2,
×2×2=2,
∴三棱锥B﹣AEG的体积为: ×2×
×2× =
= .
.
考点:1、空间直线与平面的位置关系;2、空间几何体的体积.

练习册系列答案
相关题目
 }中,各项都是正数,且3
}中,各项都是正数,且3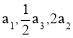 成等差数列,则
成等差数列,则 =______.
=______. 轴的正半轴为极轴建立坐标系.已知曲线
轴的正半轴为极轴建立坐标系.已知曲线
 (
( ),过点
),过点 的直线
的直线 的参数方程为
的参数方程为 (
( 是参数),直线
是参数),直线 与曲线
与曲线 分别交于
分别交于 、
、 两点.
两点. 和直线
和直线 的普通方程;
的普通方程; ,
, ,
, 成等比数列,求
成等比数列,求 的值.
的值. 的值是( )
的值是( )
 B.
B. C.
C. D.
D.
 ,
, ),半径r=
),半径r=
 .
.