题目内容
在△ABC中，角A、B、C所对边长分别为a、b、c，若a=5，b=8，B=60°，则c= ．
考点：余弦定理
专题：解三角形
分析：利用余弦定理即可得出．
解答：
解：∵a=5，b=8，B=60°，
由余弦定理可得：b2=a2+c2-2accosB，
∴82=52+c2-10ccos60°，
化为c2-5c-39=0，
解得c=
．
故答案为：
．
由余弦定理可得：b2=a2+c2-2accosB，
∴82=52+c2-10ccos60°，
化为c2-5c-39=0，
解得c=
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查了余弦定理解三角形，考查了推理能力月计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知向量是单位向量
，
，若
•
=0，且|
-
|+|
-2
|=
，则|
+2
|的取值范围是（ ）
| a |
| b |
| a |
| b |
| c |
| a |
| c |
| b |
| 5 |
| c |
| a |
| A、[1，3] | ||||||
B、[2
| ||||||
C、[
| ||||||
D、[
|
已知条件p：x2-3x-4≤0，条件q：x2-6x+9-m2≤0．若p是q的充分不必要条件，则m的取值范围是（ ）
| A、[-1，1] |
| B、[-4，4] |
| C、（-∞，-4]∪[4，+∞） |
| D、（-∞，-1]∪[4，+∞） |
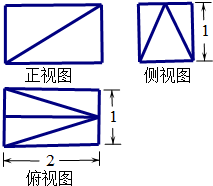
某几何体三视图如图所示，则该几何体的体积为（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|