题目内容
5.如果当|x|≤1时,所有满足|f(x)|≤1的函数f(x)=ax2+bx+c(a,b,c∈R),都有|ax+b|≤M,则最小的正数M可取为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用当|x|≤1时,所有满足|f(x)|≤1的函数f(x)=ax2+bx+c(a,b,c∈R),确定|a+b|≤2,|-a+b|≤2,结合当|x|≤1时,|ax+b|≤M,可得最小的正数M.
解答 解:∵当-1≤x≤1时,f(x)满足-1≤f(x)≤1,
∴当x=±1,x=0时,均有-1≤f(x)≤1,
即-1≤a+b+c≤1…①,-1≤c≤1②,-1≤-a+b-c≤1…③,
∴-1-c≤a+b≤1-c,-1+c≤-a+b≤1+c
∴|a+b|≤2,|-a+b|≤2,
∵当|x|≤1时,|ax+b|≤M,∴最小的正数M可取为2,
故选:B.
点评 本题主要考查了二次函数与其图象间的关系:二次函数图象上的每一点都满足二次函数的关系式.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
16.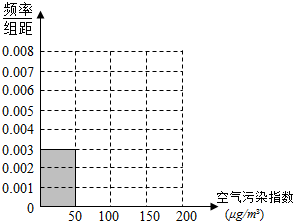 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.
当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;
当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;
当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;
当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;
当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;
当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.
2015年12月某日某省x个监测点数据统计如下:
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良,从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;
当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;
当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;
当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;
当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;
当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.
2015年12月某日某省x个监测点数据统计如下:
| 空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良,从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
13.已知tanα=2,则$\frac{sinα+2cosα}{sinα-cosα}$=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
20.在等腰梯形ABCD中,$\overrightarrow{AB}$=-2$\overrightarrow{CD}$,M为BC的中点,则$\overrightarrow{AM}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}$+$\frac{1}{4}\overrightarrow{AD}$ | D. | $\frac{1}{2}\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ |
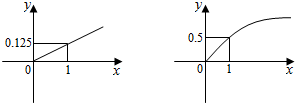 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).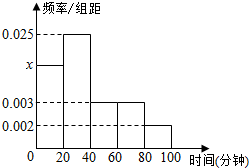 某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动
某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动