题目内容
7.已知f(x)=ex-e,则曲线y=f(x)在点(1,f(1))处的切线方程是y=ex-e.分析 欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答 解:∵f(x)=ex-e,
∴f′(x)=ex,
∴曲线y=f(x)在点(1,f(1))处的切线的斜率为:k=e,
∴曲线y=f(x)在点(1,f(1))处的切线的方程为:y=ex-e,
故答案为:y=ex-e.
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目
2.设集合A={x|y=lg(x-3)},B={y|y=2x,x∈R},则A∪B等于( )
| A. | ∅ | B. | R | C. | {x|x>1} | D. | {x|x>0} |
6.下列命题正确的是( )
| A. | 四条线段顺次首尾连接,所得的图形一定是平面图形 | |
| B. | 一条直线和两条平行直线都相交,则三条直线共面 | |
| C. | 两两平行的三条直线一定确定三个平面 | |
| D. | 和两条异面直线都相交的直线一定是异面直线 |
3.函数y=sin2x+cos2x如何平移可以得到函数y=sin2x-cos2x图象( )
| A. | 向左平移$\frac{π}{2}$ | B. | 向右平移$\frac{π}{2}$ | C. | 向左平移$\frac{π}{4}$ | D. | 向右平移$\frac{π}{4}$ |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.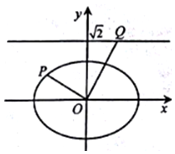 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.