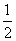题目内容
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD=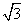 .
.
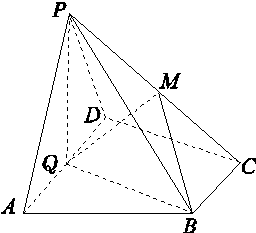
(1)求证:平面PQB⊥平面PAD;
(2)若M为棱PC的中点,求异面直线AP与BM所成角的余弦值;
(3)若二面角M-BQ-C的大小为30°,求QM的长.
解:(1)证明:证法一:∵AD∥BC,BC= AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,
∴CD∥BQ.
∵∠ADC=90°,
∴∠AQB=90°,
即QB⊥AD.
又∵平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ⊂平面PQB,
∴平面PQB⊥平面PAD.
证法二:∵AD∥BC,BC= AD,Q为AD的中点,
AD,Q为AD的中点,
∴BC∥DQ且BC=DQ,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°,
∴∠AQB=90°,即QB⊥AD.
∵PA=PD,∴PQ⊥AD.
∵PQ∩BQ=Q,
∴AD⊥平面PBQ.
∵AD⊂平面PAD,∴平面PQB⊥平面PAD.
(2)∵PA=PD,Q为AD的中点,
∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系Q-xyz,
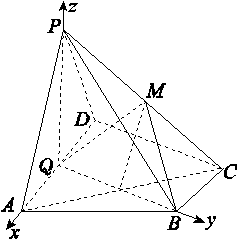
则Q(0,0,0),A(1,0,0),P(0,0,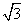 ),B(0,
),B(0,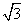 ,0),C(-1,
,0),C(-1,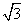 ,0).
,0).
∵M是PC的中点,
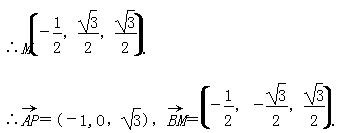 设异面直线AP与BM所成的角为θ,
设异面直线AP与BM所成的角为θ,
则cos θ=|cos〈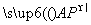 ,
,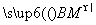 〉|
〉|
=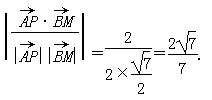
∴异面直线AP与BM所成角的余弦值为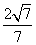 .
.
(3)由(2)知平面BQC的一个法向量为n=(0,0,1).
 ∵二面角M-BQ-C的大小为30°,
∵二面角M-BQ-C的大小为30°,
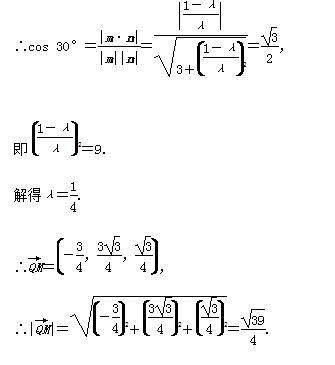 即QM的长为
即QM的长为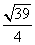 .
.

练习册系列答案
相关题目
 ,其前n项积为Tn,则T2 014=( )
,其前n项积为Tn,则T2 014=( )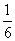 B.-
B.-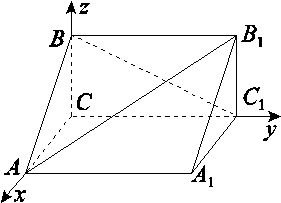
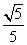 B.
B.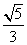 C.
C.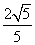 D.
D.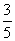

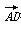 =(2,8),
=(2,8),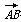 =(-3,4),对角线AC与BD相交于点M,则
=(-3,4),对角线AC与BD相交于点M,则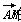 的坐标为( )
的坐标为( )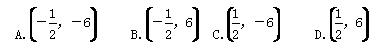
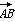 与
与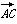 的夹角为60°,且|
的夹角为60°,且| ,则
,则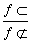 =________.
=________.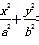 =1(a>b>0)上一点,若PF1⊥PF2,tan ∠PF2F1=2,则椭圆的离心率e=( )
=1(a>b>0)上一点,若PF1⊥PF2,tan ∠PF2F1=2,则椭圆的离心率e=( )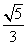 B.
B.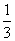 C.
C.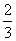 D.
D.