题目内容
19.已知复数z满足$\overline z+|z|i=3+2i$,求复数z.分析 设z=x+yi(x,y∈R),求得$\overline{z}$与|z|,代入$\overline z+|z|i=3+2i$,利用复数相等的条件得到关于x,y的方程组,求解方程组得答案.
解答 解:设z=x+yi(x,y∈R),
则$\overline{z}=x-yi$,$|z|=\sqrt{{x}^{2}+{y}^{2}}$,
代入$\overline z+|z|i=3+2i$,
得$x-yi+\sqrt{{x}^{2}+{y}^{2}}i=3+2i$,
即$\left\{\begin{array}{l}{x=3}\\{\sqrt{{x}^{2}+{y}^{2}}-y=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=\frac{5}{4}}\end{array}\right.$,
∴$z=3+\frac{5}{4}i$.
点评 本题考查复数代数形式的混合运算,考查了复数相等的条件,是基础的计算题.

练习册系列答案
相关题目
14.“x+1>0”是“x>0”成立的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
4.设函数$f(x)=\frac{(x+1)(x+a)}{x}$为奇函数,则实数a的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
11.复数z满足方程|z-1|+|z-i|=2,那么它在复平面内所表示的图形是( )
| A. | 线段 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
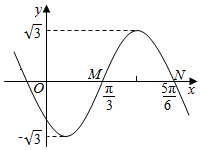 如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.
如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.