题目内容
证明下列命题:
(1)若函数f(x)可导且为周期函数,则f'(x)也为周期函数;
(2)可导的奇函数的导函数是偶函数.
证明:(1)设f(x)的周期为T,则f(x)=f(x+T).
∴f'(x)=[f(x+T)]'= f'(x+T)·(x+T)'
= f'(x+T),即f'(x)为周期函数且周期与f(x)的周期相同.
(2)∵f(x)为奇函数,
∴f(-x)=-f(x).
∴[f(-x)]'=[-f(x)]'.
∴f'(-x)·(-x)'=-f'(x).
∴f'(-x)= f'(x),即f'(x)为偶函数

练习册系列答案
相关题目
 ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当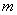 ※
※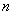 =
=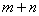 ;当
;当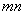 。则在此定义下,集合
。则在此定义下,集合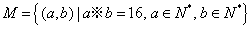 中的元素个数是
中的元素个数是  在定义域内是增函数,则实数
在定义域内是增函数,则实数 的取值范围是 .
的取值范围是 .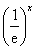 (e为自然对数的底数)成正比.当40≤x≤50时日销售量与
(e为自然对数的底数)成正比.当40≤x≤50时日销售量与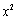 成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元. =
= ,
, =
= ,则
,则 是
是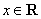 ,用
,用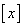 表示不超过
表示不超过 的最大整数(如
的最大整数(如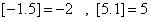 ).设
).设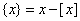 ,则对函数
,则对函数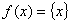 ,下列说法中正确的个数是( )
,下列说法中正确的个数是( )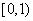
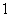 为周期的周期函数
为周期的周期函数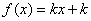 有三个不同的根,则实数
有三个不同的根,则实数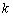 的取值范围是
的取值范围是
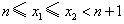
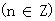 ,则
,则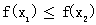
 ,使
,使 为偶函数;命题
为偶函数;命题
 ,则下列命题中为真命题的是
,则下列命题中为真命题的是 B.
B. C.
C. D.
D.
 轴正半轴且单位长度相同的极坐标系中,
轴正半轴且单位长度相同的极坐标系中,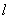 :
: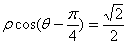 与直角坐标系中的曲线C:
与直角坐标系中的曲线C: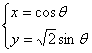 (
(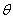 为参数),
为参数),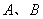 两点.
两点.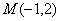 与
与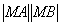 .
.