题目内容
13.给出下列三个命题(1)“若x2+2x-3≠0,则x≠1”为假命题;
(2)命题p:?x∈R,2x>0,则¬p:?x0∈R,2x0≤0
(3)“φ=$\frac{π}{2}$+kπ(k∈Z)”是“函数y=sin(2x+φ)为偶数”的充要条件.
其中正确的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 (1)根据逆否命题的等价性进行判断.
(2)根据含有量词的命题的否定进行判断.
(3)根据充分条件和必要条件的定义进行判断.
解答 解:(1)若命题“若x=1,则x2+2x-3=0”是真命题,所以其逆否命题亦为真命题,因此(1)不正确;
(2)根据含量词的命题否定方式,可知命题(2)正确.
(3)当$ϕ=\frac{π}{2}+kπ\;\;(k∈Z)$时,则函数$y=sin(2x+φ)=sin(2x+\frac{π}{2}+kπ)=±cos2x$)为偶函数;反之也成立.故“$ϕ=\frac{π}{2}+kπ\;\;(k∈Z)$”是“函数y=sin(2x+φ)为偶函数”的充要条件;综上可知:真命题的个数2.
故选:C
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但一般难度不大.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
3.已知$\overrightarrow a=(1,-2)$,$\overrightarrow b=(2,m)$,若$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow b|$=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
8.已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若?x∈(0,2]使得不等式g(2x)-ah(x)≥0恒成立,则实数a的取值范围是( )
| A. | $({-∞,2\sqrt{2}})$ | B. | $({-∞,2\sqrt{2}}]$ | C. | $({0,2\sqrt{2}}]$ | D. | $({2\sqrt{2},+∞})$ |
18.如图是一个算法的程序框图,当输入x的值为3时,输出y的结果恰好是$\frac{1}{3}$,则?处的关系式可以是( )
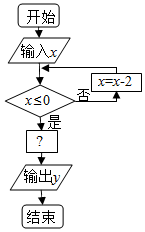

| A. | y=x2 | B. | y=3-x | C. | y=3x | D. | y=x${\;}^{\frac{1}{3}}$ |
5.在平面直角坐标系xOy中,向量$\overrightarrow{OA}$=(-1,2),$\overrightarrow{OB}$=(2,m),若O,A,B三点能构成三角形,则( )
| A. | m=-4 | B. | m≠-4 | C. | m≠1 | D. | m∈R |
2.下列命题中,真命题是( )
| A. | ?x∈R,x2≤x-2 | |
| B. | ?x∈R,2x>2-x2 | |
| C. | 函数f(x)=$\frac{1}{x}$为定义域上的减函数 | |
| D. | “被2整除的整数都是偶数”的否定是“至少存在一个被2整除的整数不是偶数” |