题目内容
14．若某正八面体的各个顶点都在半径为1的球面上，则此正八面体的体积为（ ）| A． | $\frac{32}{8}$ | B． | $\frac{32}{5}$ | C． | $\frac{8\sqrt{2}}{3}$ | D． | $\frac{4}{3}$ |
分析 将正八面体分解成两个正四棱锥，则正四棱锥的底面对角线为球的直径，高为球的半径，计算棱锥的底面边长．
解答 
解：设正八面体为ABCDEF，如图所示，则A，B，C，D四点在球的大圆上球心O在正方形ABCD的中心．
∵OA=OC=OE=1，∴AC=2，∴AB=$\sqrt{2}$．
∴正八面体的体积V=2VE-ABCD=2×$\frac{1}{3}{S}_{正方形ABCD}•OE$=2×$\frac{1}{3}×（\sqrt{2}）^{2}×1$=$\frac{4}{3}$．
故选D．
点评 本题考查了正八面体的结构特征，多面体与外接球的关系，属于基础题．
练习册系列答案
全能练考卷系列答案
相关题目
9．对任意x∈R，下列式子恒成立的是（ ）
| A． | x2-2x+1＞0 | B． | |x-1|＞0 | C． | 2x+1＞0 | D． | log2（x2+1）＞0 |
3．在三角形ABC中AB=a，AC=b（b＞0，a＞0），P是三角形ABC的外心，数量积$\overrightarrow{AP}$$•\overrightarrow{BC}$等于（ ）
| A． | $\frac{a+b}{2}$ | B． | a+b | C． | $\frac{{a}^{2}-{b}^{2}}{2}$ | D． | $\frac{{b}^{2}-{a}^{2}}{2}$ |
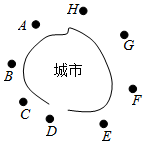某海滨城市外围有8个小岛，如图，某中学决定分两次去这8个小岛进行社会调查，每次去4个，要求每次至多只能连续两个小岛相邻（如允许ABDE，但不允许ABCE），则能够有30种安排方法．