题目内容
6.在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的方程ρ=2$\sqrt{2}$cos(θ+$\frac{π}{4}$),直线l:$\left\{\begin{array}{l}{x=2t}\\{y=at}\end{array}\right.$(t为参数)与曲线C交于A、B两点.(I)当|AB|最大时,求实数a的值;
(II)当|AB|最小时,求实数a的值.
分析 (I)把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$及其ρ2=x2+y2代入即可得到直角坐标方程,当|AB|最大时,直线l经过圆心(1,1).
(II)当|AB|最小时,直线l与圆相切,即可得出.
解答 解:(I)曲线C的方程ρ=2$\sqrt{2}$cos(θ+$\frac{π}{4}$),展开可得:ρ2=2$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(cosθ-sinθ),可得直角坐标方程:x2+y2-2x+2y=0,配方为(x-1)2+(y-1)2=2,
直线l:$\left\{\begin{array}{l}{x=2t}\\{y=at}\end{array}\right.$(t为参数)化为直角坐标方程;y=$\frac{a}{2}$x,
当|AB|最大时,直线l经过圆心(1,1),∴1=$\frac{1}{2}a$,解得a=2.
(II)当|AB|最小时,直线l与圆相切,∴$\frac{|a-2|}{\sqrt{{a}^{2}+4}}$=$\sqrt{2}$,解得a=-2.
点评 本题考查了极坐标方程与直角坐标方程的互化、直线与圆的位置关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.执行如图所示的流程图,则输出的S=( )
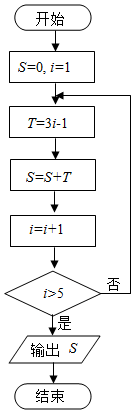

| A. | 57 | B. | 40 | C. | 26 | D. | 17 |
14.若某正八面体的各个顶点都在半径为1的球面上,则此正八面体的体积为( )
| A. | $\frac{32}{8}$ | B. | $\frac{32}{5}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4}{3}$ |
18.地球上,在北纬30°圈上有两个点A、B,它们的经度之差为180°,则A、B两点间的球面距离为(地球的半径为R)( )
| A. | $\frac{\sqrt{3}}{3}$R | B. | $\frac{1}{3}$πR | C. | $\frac{1}{2}$πR | D. | $\frac{2}{3}$πR |
16.函数f(x)=3sin(x+$\frac{π}{6}$)+$\sqrt{3}$sin($\frac{π}{3}$-x)的最大值是( )
| A. | 3 | B. | 6 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
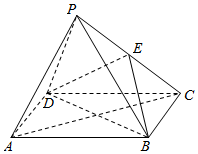 如图,四棱锥P-ABCD中,底面ABCD是边长等于2的正方形,其他四个侧面都是边长等于$\sqrt{5}$的等腰三角形,点E是PC中点.
如图,四棱锥P-ABCD中,底面ABCD是边长等于2的正方形,其他四个侧面都是边长等于$\sqrt{5}$的等腰三角形,点E是PC中点.