题目内容
1.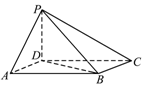 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,$∠DAB=\frac{π}{3}$,PD⊥AD,PD⊥DC.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,$∠DAB=\frac{π}{3}$,PD⊥AD,PD⊥DC.(Ⅰ)证明:平面PBC⊥平面PBD;
(Ⅱ)若二面角P-BC-D为$\frac{π}{6}$,求AP与平面PBC所成角的正弦值.
分析 (Ⅰ)推导出PD⊥BC,AD⊥BD,由AD∥BC,得BC⊥BD,从而BC⊥平面PBD,由此能证明平面PBC⊥平面PBD.
(Ⅱ)由BC⊥平面PBD,知∠PBD即为二面角P-BC-D的平面角,即∠PBD=$\frac{π}{6}$,分别以DA、DB、DP为x轴、y轴、z轴建立空间直角坐标系.利用向量法能求出AP与平面PBC所成角的正弦值.
解答 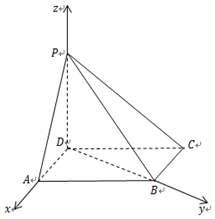 证明:(Ⅰ)∵PD⊥AD,PD⊥CDAD∩CD=D,AD?平面ABCDCD?平面ABCD
证明:(Ⅰ)∵PD⊥AD,PD⊥CDAD∩CD=D,AD?平面ABCDCD?平面ABCD
∴PD⊥平面ABCD,BC?平面ABCD
∴PD⊥BC…(2分)
又$AB=2,AD=1,∠DAB=\frac{π}{3}$
∴$BD=\sqrt{{2^2}+{1^2}-2×2×1×cos\frac{π}{3}}=\sqrt{3}$
又$\frac{BD}{sinA}=\frac{AB}{sin∠ADB}$∴$sin∠ADB=\frac{{2×\frac{{\sqrt{3}}}{2}}}{{\sqrt{3}}}=1$,
∠ADB=90°,AD⊥BD,又AD∥BC
∴BC⊥BD…(4分)
又∵PD∩BD=D,BD?平面PBD,PD?平面PBD
∴BC⊥平面PBD
而BC?平面PBC,∴平面PBC⊥平面PBD…(6分)
解:(Ⅱ)由(Ⅰ)所证,BC⊥平面PBD
∴∠PBD即为二面角P-BC-D的平面角,即∠PBD=$\frac{π}{6}$
而$BD=\sqrt{3}$,所以PD=1…(8分)
分别以DA、DB、DP为x轴、y轴、z轴建立空间直角坐标系.
则A(1,0,0),$B(0,\sqrt{3},0)$,$C(-1,\sqrt{3},0)$,P(0,0,1)
∴$\overrightarrow{AP}=(-1,0,1)$,$\overrightarrow{BC}$=(-1,0,0),$\overrightarrow{BP}=(0,-\sqrt{3},1)$,
设平面PBC的法向量为$\overrightarrow n=(x,y,z)$,
则 $\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{BC}=0}\\{\overrightarrow n•\overrightarrow{BP}=0}\end{array}}\right.$,即$\left\{\begin{array}{l}-x=0\\-\sqrt{3}y+z=0\end{array}\right.$,取y=1,得$\overrightarrow n=(0\;,\;1\;\;,\sqrt{3})$…(10分)
∴AP与平面PBC所成角的正弦值为:
$sinθ=\frac{{|{\overrightarrow{AP}•\overrightarrow n}|}}{{|{\overrightarrow{AP}}||{\overrightarrow n}|}}=\frac{{\sqrt{3}}}{{\sqrt{2}•2}}=\frac{{\sqrt{6}}}{4}$.…(12分)
点评 本题考查面面垂直的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| A. | -$\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{21}{2}$ | D. | $\frac{21}{2}$ |
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
| A. | $({-\frac{1}{2},\frac{1}{3}})$ | B. | (-1,2) | C. | $({-\frac{4}{3},-\frac{1}{2}})$ | D. | (-2,3) |
| A. | $μ=\sqrt{3},Dξ=\sqrt{7}$ | B. | $μ=\sqrt{3},Dξ=7$ | C. | μ=3,Dξ=7 | D. | $μ=3,Dξ=\sqrt{7}$ |
 如图,四棱锥P-ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD 都是边长为2的等边三角形,E 是BC的中点.
如图,四棱锥P-ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD 都是边长为2的等边三角形,E 是BC的中点.