题目内容
已知实数x，y满足不等式组
，则z=2x+y的最小值是（ ）
|
| A、2 | B、4 | C、6 | D、7 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用z的几何意义，即可得到结论．
解答：
试题分析：做出可行域，
解：作出不等式组对应的平面区域如图：
由z=2x+y得y=-2x+z，
平移直线y=-2x+z，
由图象可知当直线y=-2x+z经过点A时，直线的截距最小，
此时z最小，
由
，解得
，
即A（2，0），此时z=2×2+0=4，
故选：B
解：作出不等式组对应的平面区域如图：
由z=2x+y得y=-2x+z，
平移直线y=-2x+z，
由图象可知当直线y=-2x+z经过点A时，直线的截距最小，
此时z最小，
由
|
|
即A（2，0），此时z=2×2+0=4，
故选：B
点评：本题主要考查线性规划的应用，利用z的几何意义，利用数形结合是解决本题的关键．
练习册系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
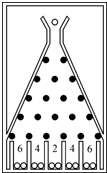在一块倾斜放置的矩形木块上钉着一个形如“等腰三角形”的五行铁钉，钉子之间留有空隙作为通道，自上而下第1行2个铁钉之间有1个空隙，第2行3个铁钉之间有2个空隙…第5行6个铁钉之间有5个空隙（如图）．某人将一个玻璃球从第1行的空隙向下滚动，玻璃球碰到第2行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙，以后玻璃球按类似方式继续往下滚动，落入第5行的某一个空隙后，掉入木板下方相应的球槽．玻璃球落入不同球槽得到的分数ξ如图所示．已知定义在R上的函数y=f（x）满足f（x+1）=f（x-1），当-1＜x≤1时，f（x）=x3，若函数g（x）=f（x）-loga|x|恰好有6个零点，则a有取值范围是（ ）
A、a∈[
| ||||
B、a∈[0，
| ||||
C、a∈[
| ||||
D、(
|
已知命题p：若xy≠4，则x≠1或y≠4，命题q：对任意实数x有x2-x+1＞0，则（ ）
| A、“p或￢q”为假命题 |
| B、“￢p且q”为真命题 |
| C、“￢p或q”为假命题 |
| D、“p且q”为真命题 |