题目内容
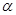 ,
,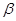 是两个不重合的平面,在下列条件中,可判定
是两个不重合的平面,在下列条件中,可判定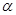 ∥
∥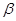 的是( )
的是( )A.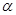 , ,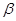 都与平面 都与平面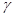 垂直 垂直 |
B.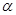 内不共线的三点到 内不共线的三点到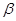 的距离相等 的距离相等 |
C.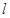 , ,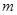 是 是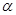 内的两条直线且 内的两条直线且 ∥ ∥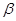 , ,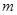 ∥ ∥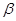 |
D.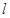 , ,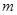 是两条异面直线且 是两条异面直线且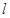 ∥ ∥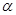 , ,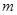 ∥ ∥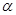 , , ∥ ∥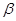 , , 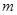 ∥ ∥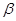 |
D
试题分析:对于A,如下图(1),
 ,但
,但 ;对于B,
;对于B, 内有不共线的三点到
内有不共线的三点到 的距离相等,此时两平面可平行(三点在平面
的距离相等,此时两平面可平行(三点在平面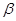 的同一侧)也可相交(三点不同在平面
的同一侧)也可相交(三点不同在平面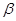 的同一侧);对于C,如下图(2),若
的同一侧);对于C,如下图(2),若 ,
, 且
且 时,不能得到
时,不能得到 ;对于D,当
;对于D,当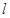 ,
,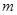 是两条异面直线且
是两条异面直线且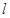 ∥
∥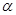 ,
,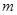 ∥
∥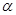 ,
, ∥
∥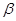 ,
, 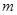 ∥
∥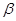 时,平面
时,平面 平面
平面 ,故选D.
,故选D.


练习册系列答案
相关题目
 中,底面
中,底面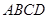 为直角梯形,
为直角梯形,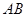 ∥
∥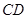 ,
, 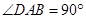 ,
,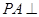 平面
平面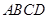 ,且
,且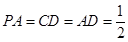 ,
,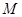 为
为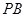 的中点
的中点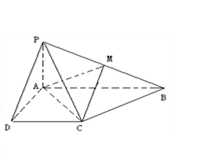
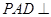 面
面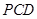
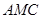 与面
与面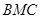 夹角的余弦值.
夹角的余弦值.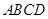 中,
中,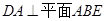 ,
,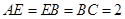 ,
,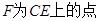 ,且
,且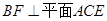 ,
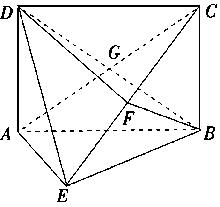
,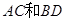 交于点
交于点 .
.
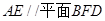 ;
;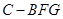 的体积.
的体积.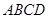 中,
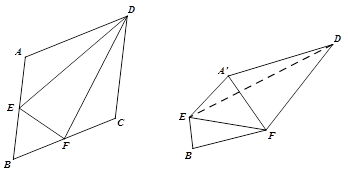
中,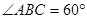 ,点
,点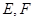 分别是
分别是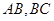 的中点,将
的中点,将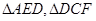 分别沿
分别沿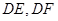 折起,使
折起,使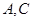 两点重合于点
两点重合于点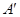 .
. (1)求证:
(1)求证: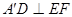 ;
;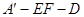 的余弦值.
的余弦值. 所在平面与正
所在平面与正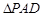 所在平面互相垂直,
所在平面互相垂直,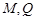 分别为
分别为 的中点.
的中点.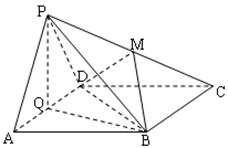
 平面
平面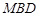 ;
;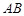 上是否存在一点
上是否存在一点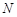 ,使得平面
,使得平面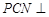 平面
平面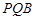 ?若存在,试指出点
?若存在,试指出点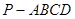 中,底面
中,底面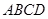 为梯形,
为梯形,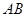 ∥
∥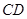 ,
, 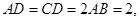
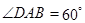 ,
,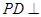 平面
平面 ,
,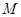 为
为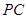 的中点
的中点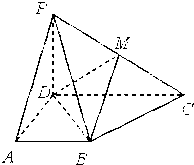
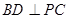
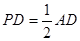 ,求二面角
,求二面角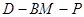 的余弦值
的余弦值 ,E,F分别是BC,AA1的中点.
,E,F分别是BC,AA1的中点.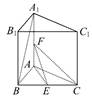
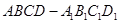 中,点
中,点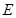 是棱
是棱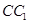 上的一个动点,平面
上的一个动点,平面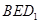 交棱
交棱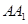 于点
于点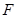 .给出下列四个结论:
.给出下列四个结论: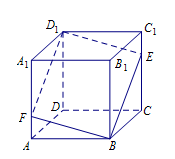
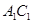 //平面
//平面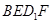 ;
;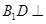 平面
平面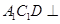 平面
平面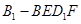 的体积均不变.
的体积均不变.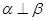 ,
,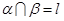 ,直线
,直线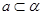 ,直线
,直线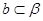 ,
,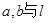 斜交,则( )
斜交,则( ) 和
和 不垂直但可能平行
不垂直但可能平行