题目内容
设直线l的方程是2x+By-1=0,倾斜角为α.
(1)试将α表示为B的函数;
(2)若
<α<
,试求B的取值范围;
(3)若B∈(-∞,-2)∪(1,+∞),求α的取值范围.
(1)试将α表示为B的函数;
(2)若
| π |
| 6 |
| 2π |
| 3 |
(3)若B∈(-∞,-2)∪(1,+∞),求α的取值范围.
(1)若B=0,则直线l的方程是2x-1=0,∴α=
;
若B≠0,则方程即为y=-
x+
,
∴当B<0时,-
>0,α=arctan(
),
当B>0时,-
<0,α=π+arctan(-
),
即:α=
(2)若α=
,则B=0,
若α≠
,则tanα<-
或tanα>
,
即-
<-
(B>0)或-
>
(B<0),
∴-2
<B<0或0<B<
.
综上,知-2
<B<
.
(3)若B<-2,则-
<1,
∴0<tanα<1,0<α<
;
若B>1,则-
>-2,
∴0>tanα>-2,π-arctan2<α<π.
综上,知π-arctan2<α<π或0<α<
.
| π |
| 2 |
若B≠0,则方程即为y=-
| 2 |
| B |
| 1 |
| B |
∴当B<0时,-
| 2 |
| B |
| -2 |
| B |
当B>0时,-
| 2 |
| B |
| 2 |
| B |
即:α=
|
(2)若α=
| π |
| 2 |
若α≠
| π |
| 2 |
| 3 |
| ||
| 3 |
即-
| 2 |
| B |
| 3 |
| 2 |
| B |
| ||
| 3 |
∴-2
| 3 |
| 2 |
| 3 |
| 3 |
综上,知-2
| 3 |
| 2 |
| 3 |
| 3 |
(3)若B<-2,则-
| 2 |
| B |
∴0<tanα<1,0<α<
| π |
| 4 |
若B>1,则-
| 2 |
| B |
∴0>tanα>-2,π-arctan2<α<π.
综上,知π-arctan2<α<π或0<α<
| π |
| 4 |

练习册系列答案
相关题目
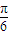 <α<
<α<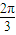 ,试求B的取值范围;
,试求B的取值范围;