题目内容
设直线l的方程是2x+By-1=0,倾斜角为α.(1)试将α表示为B的函数;
(2)若![]() <α<
<α<![]() ,试求B的取值范围;
,试求B的取值范围;
(3)若B∈(-∞,-2)∪(1,+∞),求α的取值范围.
解:(1)若B=0,则直线l的方程是2x-1=0,
∴α=![]() ;
;
若B≠0,则方程即为y=-![]() x+
x+![]() ,
,
∴当B<0时,-![]() >0,α=arctan(-
>0,α=arctan(-![]() ),
),
而当B>0时,-![]() <0,α=π+arctan(-
<0,α=π+arctan(-![]() ),
),
即α=f(B)=
(2)若α=![]() ,则B=0,
,则B=0,
若α≠![]() ,则tanα<-
,则tanα<-![]() 或tanα>
或tanα>![]() ,
,
即-![]() <-
<-![]() (B>0)或-
(B>0)或-![]() >
>![]() (B<0=,
(B<0=,
∴-2![]() <B<0或0<B<
<B<0或0<B<![]()
![]() .
.
综上,知-2![]() <B<
<B<![]()
![]() .
.
(3)若B<-2,则-![]() <1,
<1,
∴0<tanα<1,0<α<![]() ;
;
若B>1,则-![]() >-2,
>-2,
∴0>tanα>-2,π-arctan2<α<π.
综上,知π-arctan2<α<π或0<α<![]() .
.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
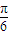 <α<
<α<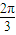 ,试求B的取值范围;
,试求B的取值范围;