题目内容
若函数f(x)=x2+(a+1)2+|x+a-1|的最小值g(a)>5.
(1)求g(a)的表达式;
(2)求a的取值范围.
(1)求g(a)的表达式;
(2)求a的取值范围.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:由已知中f(x)=x2+(a+1)2+|x+a-1|=
,分①当1-a≥
,即a≤
时,②当1-a≤-
,即a≥
时,③当-
<1-a<
,即
<a<
时,三种情况分别求出g(a)的表达式;
和满足条件的a的取值范围,最后综合讨论结果,可得答案.
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
和满足条件的a的取值范围,最后综合讨论结果,可得答案.
解答:
解:∵f(x)=x2+(a+1)2+|x+a-1|=
,
①当1-a≥
,即a≤
时,
f(x)在x<
时为减函数,在x>
时为增函数,
故g(a)=f(
)=a2-a+
>5,
解得:a<
;
②当1-a≤-
,即a≥
时,
f(x)在x<-
时为减函数,在x>-
时为增函数,
故g(a)=f(-
)=a2+3a-
>5,
解得:a≥
,
③当-
<1-a<
,即
<a<
时,
f(x)在x<1-a时为减函数,在x>1-a时为增函数,
故g(a)=f(1-a)=2a2+2>5,
解得:
<a<
,
(1)故g(a)=
(2)a的取值范围为:(-∞,
)∪(
,+∞)
|
①当1-a≥
| 1 |
| 2 |
| 1 |
| 2 |
f(x)在x<
| 1 |
| 2 |
| 1 |
| 2 |
故g(a)=f(
| 1 |
| 2 |
| 7 |
| 4 |
解得:a<
1-
| ||
| 2 |
②当1-a≤-
| 1 |
| 2 |
| 3 |
| 2 |
f(x)在x<-
| 1 |
| 2 |
| 1 |
| 2 |
故g(a)=f(-
| 1 |
| 2 |
| 1 |
| 4 |
解得:a≥
| 3 |
| 2 |
③当-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
f(x)在x<1-a时为减函数,在x>1-a时为增函数,
故g(a)=f(1-a)=2a2+2>5,
解得:
| ||
| 2 |
| 3 |
| 2 |
(1)故g(a)=
|
(2)a的取值范围为:(-∞,
1-
| ||
| 2 |
| ||
| 2 |
点评:本题考查的知识点是函数的最值及其几何意义,分段函数解析式的求法,运算量大,分类复杂,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
某扇形的圆心角为30°,半径为2,那么该扇形弧长为( )
A、
| ||
B、
| ||
C、
| ||
| D、60 |
 定义在R上的奇函数f(x),当x>0时,f(x)=x2-x-2
定义在R上的奇函数f(x),当x>0时,f(x)=x2-x-2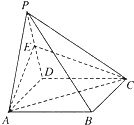 如图,已知正三角形PAD,正方形ABCD,平面PAD⊥平面ABCD,E为PD的中点.
如图,已知正三角形PAD,正方形ABCD,平面PAD⊥平面ABCD,E为PD的中点.