题目内容

已知θ为锐角，sinθ=
5
5
，则sin（θ+
π
2
）等于（　　）
A、
3
5
B、
10
5
C、
2
5
D、
2
5
5
考点：两角和与差的正弦函数
专题：计算题,三角函数的求值
分析：运用同角三角函数的平方关系式，求出cosθ，再运用
π
2
+θ的诱导公式即可．
解答： 解：∵θ为锐角，sinθ=
5
5
，
∴cosθ=
1-sin2θ
=
1-(
5
5
)2
=
2
5
5
，
∴sin（θ+
π
2
）=cosθ=
2
5
5
．
故选D．
点评：本题考查同角三角函数的基本关系式：平方关系，以及诱导公式的运用，考查基本运算能力，属于基础题．
练习册系列答案
相关题目
已知复数z满足z=
2i
1+i
，那么z在复平面上对应的点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
已知O是坐标原点，点A（-1，0），若M（x，y）为平面区域
x+y≥2
x≤1
y≤2
上的一个动点，则|
OA
+
OM
|的最小值是（　　）
A、
2
2
B、1
C、
3
2
2
D、
5
双曲线的一个顶点为（2，0），一条渐近线方程为y=
2
x，则该双曲线的方程是（　　）
A、
x2
4
-
y2
2
=1
B、
x2
2
-
y2
4
=1
C、
y2
8
-
x2
4
=1
D、
x2
4
-
y2
8
=1
各大学在高考录取时采取专业志愿优先的录取原则．一考生从某大学所给的7个专业中，选择3个作为自己的第一、二、三专业志愿，其中甲、乙两个专业不能同时兼报，则该考生不同的填报专业志愿的方法有（　　）
A、210种B、180种
C、120种D、95种
复数z的虚部为1，且
z
1+i
为纯虚数，其中i是虚数单位，则z=（　　）
A、-1-iB、1+i
C、1-iD、-1+i
已知函数f（x）=|x-1|．
（Ⅰ）解不等式：f（x）+f（x-1）≤2；
（Ⅱ）当a＞0时，不等式2a-3≥f（ax）-af（x）恒成立，求实数a的取值范围．
已知x=1是函数f（x）=（ax-2）ex（a∈R）的一个极值点，
（Ⅰ）求a的值；
（Ⅱ）若x∈[0，2]，有t-e≤f（x）恒成立，求t的取值范围．
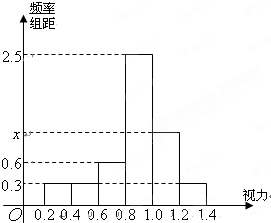为了解某校高三学生的视力情况，随机抽查了该校50名高三学生，得到如图所示的频率分布直方图．
（Ⅰ）求图中x的值；
（Ⅱ）若从视力在[0.2，0.6）的学生中随机选取2人，求这2人视力均在[0.2，0.4）的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网