从4男2女共6名学生中选派2人参加某项爱心活动.则所选2人中至少有1名女生的概率为$\frac{3}{5}$．题目和参考答案——青夏教育精英家教网——

题目内容

11．从4男2女共6名学生中选派2人参加某项爱心活动，则所选2人中至少有1名女生的概率为$\frac{3}{5}$．

分析所选2人中至少有1名女生的对立事件是所选两人中没有女生，由此能求出所选2人中至少有1名女生的概率．

解答解：所选2人中至少有1名女生的对立事件是所选两人中没有女生，
∴所选2人中至少有1名女生的概率为p=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=1-$\frac{6}{15}$=$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．

点评本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．

练习册系列答案

暑假作业浙江教育出版社系列答案

学霸训练系列答案

尖子生课课练系列答案

七彩的假期生活暑假系列答案

蓝博士暑假作业甘肃少年儿童出版社系列答案

快乐暑假新疆美术摄影出版社系列答案

中考快递课课帮系列答案

名校之约暑假作业系列答案

课时练提速训练系列答案

暑假作业光明日报出版社系列答案

相关题目

1．对于实数x，符号[x]表示不超过x的最大整数，例如[π]=3，[-1.08]=-2，如果定义函数f（x）=x-[x]，那么下列命题中正确的序号有（　　）
①f（x）的定义域为R，值域为[0，1]②f（x）在区间[0，1）上单调递增
③f（x）既不是奇函数也不是偶函数 ④函数f（x）与g（x）=log₅（-x）图象有5个交点．

2．已知m∈R，向量$\overrightarrow a=（m，1）$，$\overrightarrow b=（2，-6）$，且$\overrightarrow a⊥\overrightarrow b$，则$|\overrightarrow a-\overrightarrow b|$=$5\sqrt{2}$．

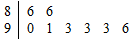如图是某班8位学生诗词比赛得分的茎叶图，那么这8位学生得分的众数和中位数分别为93、92．

6．已知点A（-3，2），在直线y=-x点找一点B，在x轴上找一点C，使此三点构成三角形，则△ABC的周长的最小值为$\sqrt{26}$．

16．各项均为正数的等比数列{a_n}的前n项和为S_n，若a₃=2，S₄=5S₂，则S₄=$\frac{15}{2}$．

3．根据函数y=f（x）的图象，求：f（0），f（3），定义域D，值域M，最值，单调减区间．

20．设向量$\overrightarrow{a}$=（2，-4），$\overrightarrow{b}$=（6，x），若|$\overrightarrow{a}+\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|，则x=（　　）

1．若复数z=（3+bi）（1+i）-2是纯虚数（b∈R），则|z|=（　　）