题目内容
1.求矩阵$[\begin{array}{l}{2}&{0}&{2}&{2}&{1}\\{1}&{3}&{-1}&{0}&{-1}\\{2}&{1}&{0}&{1}&{-1}\\{-1}&{1}&{2}&{3}&{2}\end{array}]$的秩.分析 (1)根据矩阵的初等行变换,将其化成上三角,再求矩阵的秩,(2)可以通过观察矩阵是否行或列成比例,没有则是满秩.
解答 解:矩阵的秩为非零子式的最高阶数,通过观察,没有两行或两列成比例,因此矩阵是满秩,因此此矩阵的秩为4.
点评 主要考察矩阵的性质,可以通过观察求出矩阵的秩.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(x,4),则x=-2是$\overrightarrow{a}$∥$\overrightarrow{b}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知3tan$\frac{α}{2}$+$ta{n}^{2}\frac{α}{2}$=1,sinβ=3sin(2α+β),则tan(α+β)=( )
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | -3 |
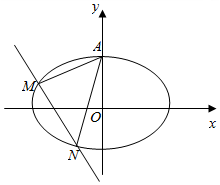 过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.
过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.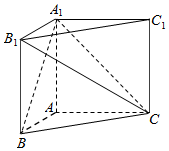 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.