题目内容
13.如图1,已知等腰梯形ABCD中,AD∥BC,AB=AD=$\frac{1}{2}$BC=2,E是BC的中点,AE∩BD=M,将△BAE沿着AE翻折成图2△B1AE.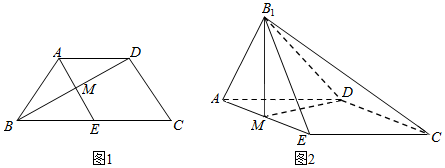
(Ⅰ)求证:CD⊥平面B1DM;
(Ⅱ)若B1C=$\sqrt{10}$,求棱锥B1-CDE的体积.
分析 (1)由题意可知四边形ABED是菱形,四边形AECD是平行四边形,故CD∥AE.AE⊥B1M,AE⊥DM,故而AE⊥平面B1DM,从而CD⊥平面B1DM;
(2)由条件可知△ABE,△ADE,△CDE是等边三角形,求出B1M,DM,CM,由勾股定理可证B1M⊥MC,于是B1M⊥平面AECD,即B1M为棱锥的高.
解答 (I)证明:连接DE,∵AD∥BC,AB=AD=$\frac{1}{2}$BC=BE=CE=CD,
∴四边形ABED和AECD是菱形,
∴AE∥CD,BM⊥AM,DM⊥AM,即B1M⊥AE,DM⊥AE,
又∵DM∩B1M=M,MD?平面B1MD,B1M?平面B1MD,
∴AE⊥平面B1MD.∵AE∥CD,
∴CD⊥平面B1DM.
(Ⅱ) 连接CM,∵AB=AD=AE=BE=CE=CD=DE=2,AE⊥BD,
∴B1M=DM=$\sqrt{3}$.S△CDE=$\frac{\sqrt{3}}{4}$×22=$\sqrt{3}$.
∴CM=$\sqrt{C{D}^{2}+D{M}^{2}}=\sqrt{7}$,∵B1C=$\sqrt{10}$,
∴B1M2+CM2=B1C2,∴B1M⊥CM,
又B1M⊥AE,MC∩AE=M,
∴B1M⊥平面CDE.
∴V${\;}_{{B}_{1}-CDE}$=$\frac{1}{3}$S△CDE•B1M=$\frac{1}{3}×\sqrt{3}×\sqrt{3}$=1.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
2.实数x,y满足条件$\left\{\begin{array}{l}{3x-6y-2≤0}\\{|x|+|y|≤1}\end{array}\right.$,则z=2x-y的取值范围是( )
| A. | [-2,$\frac{5}{3}$] | B. | [-$\frac{1}{3}$,2] | C. | [-$\frac{1}{3}$,$\frac{5}{3}$] | D. | [-2,2] |
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$与函数y=$\sqrt{x}$的图象交于点P,若函数y=$\sqrt{x}$的图象在点P处的切线过双曲线左焦点F(-2,0),则双曲线的离心率是( )
| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\frac{3}{2}$ |
3.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点到一条渐近线的距离不大于$\frac{{\sqrt{5}}}{3}c$(c为双曲线的半焦距长),则双曲线离心率的取值范围为( )
| A. | $[\frac{{3\sqrt{5}}}{2},+∞)$ | B. | $(1,\frac{3}{2}]$ | C. | $(1,\frac{{3\sqrt{5}}}{2}]$ | D. | $[\frac{3}{2},+∞)$ |