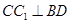题目内容
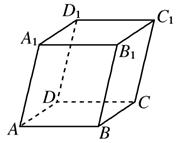
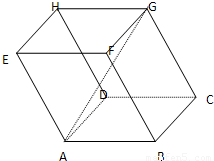
 如图,平行六面体ABCD-A1B1C1D1中,侧棱B1B长为3,底面是边长为2的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,则AE+C1E的最小值为( )
如图,平行六面体ABCD-A1B1C1D1中,侧棱B1B长为3,底面是边长为2的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,则AE+C1E的最小值为( )分析:将面C1CB1B,B1BAA1打开,连接AC1,C1B,则AC1为AE+C1E的最小值,由此利用题设条件能求出结果.
解答:解:将面C1CB1B,B1BAA1打开,如图,由已知得C,B,A共线,
连接AC1,则AC1为AE+C1E的最小值,
平行六面体中,侧棱B1B长为3,底面是边长为2的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,
∴∠C1BB1=30°,∠B1BA=60°,则∠ABC1=90°,
在三角形C1BC中由余弦定理得C1B=4,
∴C1A2=C1B2+AB2=42+22=20,
∴C1A=
=2
,
故AE+C1E的最小值为2
.
故选:C.

连接AC1,则AC1为AE+C1E的最小值,
平行六面体中,侧棱B1B长为3,底面是边长为2的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,
∴∠C1BB1=30°,∠B1BA=60°,则∠ABC1=90°,
在三角形C1BC中由余弦定理得C1B=4,
∴C1A2=C1B2+AB2=42+22=20,
∴C1A=
| 20 |
| 5 |
故AE+C1E的最小值为2
| 5 |
故选:C.
点评:本题考查线段和最小值的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
 如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为
如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为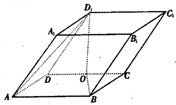 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.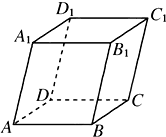 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,