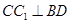题目内容
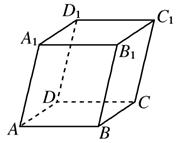
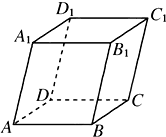如图，平行六面体ABCD-A1B1C1D1中，∠BAD=∠BAA1=∠DAA1=60°，（1）当AA1=3，AB=2，AD=2，求AC1的长；
（2）当底面ABCD是菱形时，求证：CC1⊥BD．
分析：（1）利用空间向量的加法法则可得
=
+
+
，再利用数量积的性质可得
2=(
+
+
)2=
2+
2+
2+2
•
+2
•
+2
•
，再利用数量积的性质即可得出．
（2）连接AC、BD，相交于点O．利用菱形的性质可得AC⊥BD．OD=OB．再连接A1B，A1D，A1O．利用已知可证明△A1AB≌△A1AD，得到A1B=A1D，利用等腰三角形的性质可得A1O⊥BD．再利用线面垂直的判定定理即可证明结论．
| AC1 |
| AB |
| AD |
| AA1 |
| AC1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
（2）连接AC、BD，相交于点O．利用菱形的性质可得AC⊥BD．OD=OB．再连接A1B，A1D，A1O．利用已知可证明△A1AB≌△A1AD，得到A1B=A1D，利用等腰三角形的性质可得A1O⊥BD．再利用线面垂直的判定定理即可证明结论．
解答：（1）解：如图所示．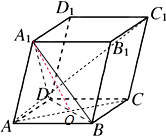
∵|
|=|
|=2，|
|=3，∠BAD=∠BAA1=∠DAA1=60°，
∴
•
=|
|•|
|×cos60°=2×2×
=2，
•
=
•
=|
|•|
|×cos60°=2×3×
=3，
∵
=
+
+
，
∴
2=(
+
+
)2=
2+
2+
2+2
•
+2
•
+2
•
=22+22+32+2×2+2×2×3=33．
∴|
|=
；
（2）证明：连接AC、BD，相交于点O．∵底面ABCD是菱形，∴AC⊥BD．OD=OB．
再连接A1B，A1D，A1O．在△A1AB和△A1AD中，∵AB=AD，∠BAA1=∠DAA1=60°，AA1公用，
∴△A1AB≌△A1AD，∴A1B=A1D，又OD=OB，∴A1O⊥BD．
∵A1O与CC1是相交直线，∴BD⊥对角面ACC1A1．
∴BD⊥CC1．
∵|
| AB |
| AD |
| AA1 |
∴
| AB |
| AD |
| AB |
| AD |
| 1 |
| 2 |
| AB |
| AA1 |
| AD |
| AA1 |
| AD |
| AA1 |
| 1 |
| 2 |
∵
| AC1 |
| AB |
| AD |
| AA1 |
∴
| AC1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
=22+22+32+2×2+2×2×3=33．
∴|
| AC1 |
| 33 |
（2）证明：连接AC、BD，相交于点O．∵底面ABCD是菱形，∴AC⊥BD．OD=OB．
再连接A1B，A1D，A1O．在△A1AB和△A1AD中，∵AB=AD，∠BAA1=∠DAA1=60°，AA1公用，
∴△A1AB≌△A1AD，∴A1B=A1D，又OD=OB，∴A1O⊥BD．
∵A1O与CC1是相交直线，∴BD⊥对角面ACC1A1．
∴BD⊥CC1．
点评：本题综合考查了空间向量的加法法则、数量积的性质、菱形的性质、三角形的全等判定与性质、等腰三角形的性质、线面垂直的判定与性质等基础知识与基本技能方法，属于难题．
练习册系列答案
相关题目
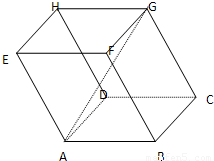
如图，平行六面体ANCD-EFGH中，棱AB，AD，AE的长分别为3，4，5，∠EAD=∠EAB=∠DAB=120°，则AG的长为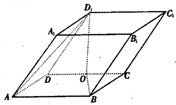
如图，平行六面体ABCD-A1B1C1D1中，AB=2，AD=1，底面ABCD是矩形，顶点D1在底面ABCD上的射影O恰好是CD的中点．
