题目内容
如图，平行六面体ANCD-EFGH中，棱AB，AD，AE的长分别为3，4，5，∠EAD=∠EAB=∠DAB=120°，则AG的长为分析：先把所求问题转化为求向量AG的长度，再根据向量的三角形法则以及其为平行六面体得到
=
+
+
=
+
+
；再对等式两边平方即可找到结论．
| AG |
| AB |
| BC |
| CG |
| AB |
| AD |
| AE |
解答：解：因为其为平行六面体
所以
=
+
+
=
+
+
．
∴
2=(
+
+
)2
=
2 +
2 +
2+2
•
+2
•
+2
•
=32+42+52+2×3×4×cos120°+2×3×5×cos120°+2×4×5×cos120°
=50-12-15-20=3．
∴|
|=
．
故答案为：
．
所以
| AG |
| AB |
| BC |
| CG |
| AB |
| AD |
| AE |
∴
| AG |
| AB |
| AD |
| AE |
=
| AB |
| AD |
| AE |
| AB |
| AD |
| AB |
| AE |
| AD |
| AE |
=32+42+52+2×3×4×cos120°+2×3×5×cos120°+2×4×5×cos120°
=50-12-15-20=3．
∴|
| AG |
| 3 |
故答案为：
| 3 |
点评：本题主要考查求两点间的距离问题．解决本题的关键在于根据向量的三角形法则以及其为平行六面体得到
=
+
+
=
+
+
．
| AG |
| AB |
| BC |
| CG |
| AB |
| AD |
| AE |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
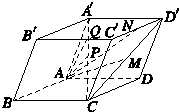如图所示，在平行六面体ABCD-A′B′C′D′中，