题目内容
3.已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的焦距为4,左、右焦点分别为F1、F2,且C1与抛物线C2:y2=x的交点所在的直线经过F2.(Ⅰ)求椭圆C1的方程;
(Ⅱ)过F1的直线l与C1交于A,B两点,与抛物线C2无公共点,求△ABF2的面积的取值范围.
分析 (Ⅰ)依题意可得F1F2的坐标,由此可得椭圆C1与抛物线C2的一个交点为$P({2,\sqrt{2}})$,由椭圆的定义可得a的值,又由a2=b2+c2,解得b的值,将其代入椭圆的方程即可得答案;
(Ⅱ)依题意,直线l:x=ty-2,联立直线与抛物线的方程整理可得y2-ty+2=0,联立直线与椭圆的方程可得(t2+2)y2-4ty-4=0,进而设A(x1,y1),B(x2,y2),由根与系数的关系分析可得|AB|的长度以及F2到直线l距离d,进而可以表示△ABF2的面积,借助换元法分析可得答案.
解答 解:(Ⅰ)依题意得2c=4,则F1(2,0)F2(-2,0);
所以椭圆C1与抛物线C2的一个交点为$P({2,\sqrt{2}})$,
于是2a=|PF1|$+|{P{F_2}}|=4\sqrt{2}$,从而$a=2\sqrt{2}$.
又a2=b2+c2,解得b=2
所以椭圆C1的方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$.
(Ⅱ)依题意,直线l的斜率不为0,设直线l:x=ty-2,
由$\left\{\begin{array}{l}x=ty-2\\{y^2}=x\end{array}\right.$,消去x整理得y2-ty+2=0,由△=(-t)2-8<0得t2<8.
由$\left\{\begin{array}{l}x=ty-2\\{x^2}+2{y^2}=8\end{array}\right.$,消去x整理得(t2+2)y2-4ty-4=0,
设A(x1,y1),B(x2,y2),则${y_1}+{y_2}=\frac{4t}{{{t^2}+2}}$,${y_1}{y_2}=-\frac{4}{{{t^2}+2}}$,
所以$|{AB}|=\sqrt{1+{t^2}}|{{y_1}-{y_2}}|$=$\sqrt{1+{t^2}}\sqrt{{{({{y_1}+{y_2}})}^2}-4{y_1}{y_2}}$=$\frac{{4\sqrt{2}({{t^2}+1})}}{{{t^2}+2}}$,F2到直线l距离$d=\frac{4}{{\sqrt{{t^2}+1}}}$,
故${S_{AB{F_2}}}=\frac{1}{2}|{AB}|d$=$\frac{1}{2}•\frac{{4\sqrt{2}({{t^2}+1})}}{{{t^2}+2}}•\frac{4}{{\sqrt{{t^2}+1}}}$=$\frac{{8\sqrt{2}\sqrt{{t^2}+1}}}{{{t^2}+2}}$,
令$\sqrt{{t^2}+1}=s∈[{1,3})$,则${S_{AB{F_2}}}=\frac{{8\sqrt{2}\sqrt{{t^2}+1}}}{{{t^2}+2}}$=$\frac{{8\sqrt{2}s}}{{{s^2}+1}}=\frac{{8\sqrt{2}}}{{s+\frac{1}{s}}}$$∈({\frac{{12\sqrt{2}}}{5},4\sqrt{2}}]$,
所以三边形ABF2的面积的取值范围为$({\frac{{12\sqrt{2}}}{5},4\sqrt{2}}]$.
点评 本题考查直线与椭圆、抛物线的位置关系,涉及椭圆的几何性质,关键是正确求出椭圆的标准方程.

| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
| A. | (-∞,1-e) | B. | (1-e,1] | C. | [1,e-1) | D. | (e-1,+∞) |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为ξ,求ξ的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{7}{5}=1.4$,$\widehata=\overline y-\widehatb\overline x$,其中$\overline x,\overline y$为样本均值.
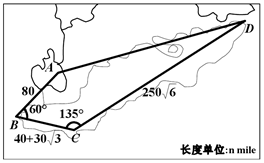 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.