题目内容
如果对任意实数x,y,都有f(x+y)=f(x)·f(y),且f(1)=2,
(1)求f(2),f(3),f(4)的值.
(2)求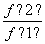 +
+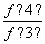 +
+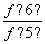 +…+
+…+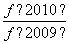 +
+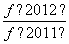 +
+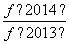 +
+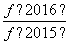 的值.
的值.
解 (1)因为对任意实数x,y,
都有f(x+y)=f(x)·f(y),且f(1)=2,
所以f(2)=f(1+1)=f(1)·f(1)=22=4,
f(3)=f(2+1)=f(2)·f(1)=23=8,
f(4)=f(3+1)=f(3)·f(1)=24=16.
(2)由(1)知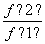 =2,
=2,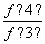 =2,
=2,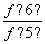 =2,…,
=2,…,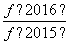 =2.
=2.
故原式=2×1 008=2 016.

练习册系列答案
相关题目
 关于直线
关于直线 对称的直线方程为
对称的直线方程为  =
= ,则当x≠0且x≠1时,f(x)=( )
,则当x≠0且x≠1时,f(x)=( ) B.
B.
 D.
D.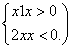
 的定义域是________.
的定义域是________.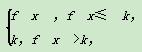 取函数f(x)=2-|x|.当k=
取函数f(x)=2-|x|.当k=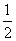 时,函数fk(x)的单调递增区间为( )
时,函数fk(x)的单调递增区间为( ) 成立,则实数a的取值范围是( )
成立,则实数a的取值范围是( )