题目内容
已知f(x)=x2-1,g(x)=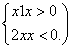
(1)求f(g(2))和g(f(2))的值;
(2)求f(g(x))和g(f(x))的解析式.
解 (1)由已知,g(2)=1,f(2)=3,
因此f(g(2))=f(1)=0,
g(f(2))=g(3)=2.
(2)当x>0时,g(x)=x-1,
故f(g(x))=(x-1)2-1=x2-2x;
当x<0时,g(x)=2-x,
故f(g(x))=(2-x)2-1=x2-4x+3.
所以f(g(x))=
当x>1或x<-1时,f(x)>0,
故g(f(x))=f(x)-1=x2-2;
故-1<x<1时,f(x)<0,
故g(f(x))=2-f(x)=3-x2.
所以g(f(x))=

练习册系列答案
相关题目
 与点
与点 关于
关于 轴对称,而点
轴对称,而点 关于原点对称,则点
关于原点对称,则点 B.
B. C.
C. D.
D.
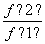 +
+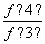 +
+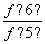 +…+
+…+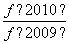 +
+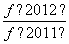 +
+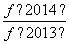 +
+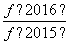 的值.
的值. 的定义域为R,则实数m的取值范围是( )
的定义域为R,则实数m的取值范围是( ) B.
B.
 D.
D.