题目内容
设函数y＝f(x)在(－∞，＋∞)内有定义．对于给定的正数k，定义函数fk(x)＝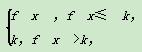
取函数f(x)＝2－|x|.当k＝
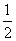时，函数fk(x)的单调递增区间为( )
A．(－∞，0) B．(0，＋∞)
C．(－∞，－1) D．(1，＋∞)
C解析 由f(x)>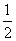，得－1<x<1.
由f(x)≤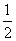，得x≤－1或x≥1.
所以f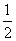(x)＝
故f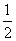(x)的单调递增区间为(－∞，－1)．
练习册系列答案
相关题目
题目内容
设函数y＝f(x)在(－∞，＋∞)内有定义．对于给定的正数k，定义函数fk(x)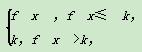＝取函数f(x)＝2－|x|.当k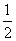＝时，函数fk(x)的单调递增区间为( )
A．(－∞，0) B．(0，＋∞)
C．(－∞，－1) D．(1，＋∞)
C解析 由f(x)>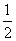，得－1<x<1.
由f(x)≤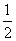，得x≤－1或x≥1.
所以f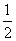(x)＝
故f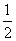(x)的单调递增区间为(－∞，－1)．
＋
＋
＋…＋
＋
＋
＋
的值．
例如：34＝3，(－2)4＝4，则函数f(x)＝x2(2x－x2)的最大值为________．
f(x)＝2 014，且当x∈
时，f(x)＝log2(2x＋1)，则f(－2 015)＋f(2 013)＝________.
＋
的最小值是________．
的图象可能是( )