题目内容
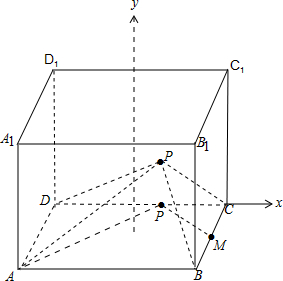
在正方体ABCD-A1B1C1D1中,M是BC的中点,点P是面DCC1D1所在的平面内的动点,且满足∠APD=∠MPC,则点P的轨迹是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
考点:轨迹方程
专题:直线与圆,空间位置关系与距离
分析:由题意画出图形,由角的关系得到边的关系,建系后由求轨迹方程的方法求得P的轨迹.
解答:
解:如图,∠APD=∠MPC,
在Rt△PDA与Rt△PCM中,设AD=2,则MC=1,
∴tanAPD=
=
,则
=
,PD=2PC.
在平面DCC1D1中,以DC所在直线为x轴,以DC的垂直平分线为y轴建立平面直角坐标系,
则D(-1,0),C(1,0),
设P(x,y),
由PD=2PC,得:
=2
,
整理得:x2-
x+y2+1=0.
∴点P的轨迹是圆.
故选:A.
在Rt△PDA与Rt△PCM中,设AD=2,则MC=1,
∴tanAPD=
| AD |
| PD |
| MC |
| PC |
| 2 |
| PD |
| 1 |
| PC |
在平面DCC1D1中,以DC所在直线为x轴,以DC的垂直平分线为y轴建立平面直角坐标系,
则D(-1,0),C(1,0),
设P(x,y),
由PD=2PC,得:
| (x+1)2+y2 |
| (x-1)2+y2 |
整理得:x2-
| 10 |
| 3 |
∴点P的轨迹是圆.
故选:A.

点评:本题考查了轨迹方程的求法,考查了数学转化思想方法,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
已知复合命题p∧(¬q)是真命题,则下列命题中也是真命题的是( )
| A、(¬p)∨q |
| B、p∨q |
| C、p∧q |
| D、(¬p)∧(¬q) |
已知命题P:“若x≥a2+b2,则x≥2ab”,则下列说法正确的是( )
| A、命题P的逆命题是“若x<a2+b2,则x<2ab” |
| B、命题P的逆命题是“若x<2ab,则x<a2+b2” |
| C、命题P的否命题是“若x<a2+b2,则x<2ab” |
| D、命题P的否命题是“若x≥a2+b2,则x<2ab” |