题目内容
若△ABC的面积为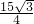 ,AB=3,AC=5,且角A为钝角,边BC的中点为D,则AD长度为
,AB=3,AC=5,且角A为钝角,边BC的中点为D,则AD长度为
- A.

- B.
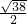
- C.

- D.7
A
分析:由△ABC的面积求得sinA= ,再由角A为钝角,可得A=
,再由角A为钝角,可得A= .△ABC中,由余弦定理求得BC=7,再由正弦定理求得sinB的值.由题意可得B为锐角,利用同角三角函数的
.△ABC中,由余弦定理求得BC=7,再由正弦定理求得sinB的值.由题意可得B为锐角,利用同角三角函数的
基本关系求得cosB 的值,△ABD中,由余弦定理求得AD的值.
解答:△ABC中,由题意可得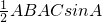 =
=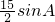 =
=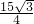 ,∴sinA=
,∴sinA= .
.
再由角A为钝角,可得A= .
.
由余弦定理可得 BC2=AB2+AC2-2•AB•AC•cosA=9+25-30•cos =49,∴BC=2BD=7.
=49,∴BC=2BD=7.
再由正弦定理可得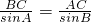 ,即
,即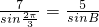 ,∴sinB=
,∴sinB=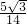 .
.
由题意可得B为锐角,∴cosB=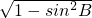 =
= .
.
△ABD中,由余弦定理可得 AD2=AB2+BD2-2•AB•BD•cosB=9+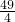 -21•
-21• =
= ,∴AD=
,∴AD= ,
,
故选A.
点评:本题主要考查正弦定理和余弦定理的应用,已知三角函数值求角的大小,属于中档题.
分析:由△ABC的面积求得sinA=
 ,再由角A为钝角,可得A=
,再由角A为钝角,可得A= .△ABC中,由余弦定理求得BC=7,再由正弦定理求得sinB的值.由题意可得B为锐角,利用同角三角函数的
.△ABC中,由余弦定理求得BC=7,再由正弦定理求得sinB的值.由题意可得B为锐角,利用同角三角函数的基本关系求得cosB 的值,△ABD中,由余弦定理求得AD的值.
解答:△ABC中,由题意可得
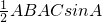 =
=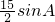 =
=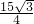 ,∴sinA=
,∴sinA= .
.再由角A为钝角,可得A=
 .
.由余弦定理可得 BC2=AB2+AC2-2•AB•AC•cosA=9+25-30•cos
 =49,∴BC=2BD=7.
=49,∴BC=2BD=7.再由正弦定理可得
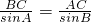 ,即
,即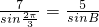 ,∴sinB=
,∴sinB=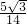 .
.由题意可得B为锐角,∴cosB=
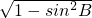 =
= .
.△ABD中,由余弦定理可得 AD2=AB2+BD2-2•AB•BD•cosB=9+
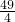 -21•
-21• =
= ,∴AD=
,∴AD= ,
,故选A.
点评:本题主要考查正弦定理和余弦定理的应用,已知三角函数值求角的大小,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
P是△ABC所在平面上的一点,且满足
+
+2
=0,若△ABC的面积为1,则△PAB的面积为( )
| PA |
| PB |
| PC |
A、
| ||
B、
| ||
C、
| ||
D、
|