题目内容
1. 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=b2,已知椭圆C的离心率为$\frac{{2\sqrt{2}}}{3}$,直线$\sqrt{2}$x-2y-$\sqrt{6}$=0与圆O相切.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=b2,已知椭圆C的离心率为$\frac{{2\sqrt{2}}}{3}$,直线$\sqrt{2}$x-2y-$\sqrt{6}$=0与圆O相切.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)椭圆C的上顶点为B,EF是圆O的一条直径,EF不与坐标轴重合,直线BE、BF与椭圆C的另一个交点分别为P、Q,求△BPQ的面积的最大值及此时PQ所在的直线方程.
分析 (1)直线$\sqrt{2}$x-2y-$\sqrt{6}$=0与圆O相切,则b=r=$\frac{丨\sqrt{2}×0-2×0-\sqrt{6}丨}{\sqrt{(\sqrt{2})^{2}+(-2)^{2}}}$=1,由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{2\sqrt{2}}}{3}$,解得:a2,
(Ⅱ)由题意知直线BP,BQ的斜率存在且不为0,BP⊥BQ,不妨设直线BP的斜率为k(k>0),则PE:y=kx+1.由$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,得P(-$\frac{18k}{9{k}^{2}+1}$,$-\frac{9{k}^{2}-1}{9{k}^{2}+1}$).用-$\frac{1}{k}$代替k,Q($\frac{18k}{{k}^{2}+9}$,-$\frac{9-{k}^{2}}{{k}^{2}+9}$),则丨PB丨=$\sqrt{(0+\frac{18k}{9{k}^{2}+1})^{2}+(1+\frac{9{k}^{2}-1}{9{k}^{2}+1})^{2}}$=$\frac{18k}{9{k}^{2}+1}$•$\sqrt{1+{k}^{2}}$,丨BQ丨$\sqrt{(0-\frac{18k}{{k}^{2}+9})^{2}+(1+\frac{9-{k}^{2}}{{k}^{2}+9})^{2}}$=$\frac{18}{9+{k}^{2}}$•$\sqrt{1+{k}^{2}}$,S△BPQ=$\frac{1}{2}$×丨PB丨×丨BQ丨=$\frac{1}{2}$×$\frac{18k}{9{k}^{2}+1}$•$\sqrt{1+{k}^{2}}$×$\frac{18}{9+{k}^{2}}$•$\sqrt{1+{k}^{2}}$,即可求解,
解答 解:(1)直线$\sqrt{2}$x-2y-$\sqrt{6}$=0与圆O相切,则b=r=$\frac{丨\sqrt{2}×0-2×0-\sqrt{6}丨}{\sqrt{(\sqrt{2})^{2}+(-2)^{2}}}$=1,
由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{2\sqrt{2}}}{3}$,解得:a2=9,
椭圆的标准方程:$\frac{{x}^{2}}{9}+{y}^{2}=1$;
(Ⅱ)由题意知直线BP,BQ的斜率存在且不为0,BP⊥BQ,不妨设直线BP的斜率为k(k>0),
则PE:y=kx+1.
由$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-\frac{18k}{9{k}^{2}+1}}\\{y=\frac{-9{k}^{2}+1}{9{k}^{2}+1}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$,
∴P(-$\frac{18k}{9{k}^{2}+1}$,$-\frac{9{k}^{2}-1}{9{k}^{2}+1}$).
用-$\frac{1}{k}$代替k,Q($\frac{18k}{{k}^{2}+9}$,-$\frac{9-{k}^{2}}{{k}^{2}+9}$),
则丨PB丨=$\sqrt{(0+\frac{18k}{9{k}^{2}+1})^{2}+(1+\frac{9{k}^{2}-1}{9{k}^{2}+1})^{2}}$=$\frac{18k}{9{k}^{2}+1}$•$\sqrt{1+{k}^{2}}$,
丨BQ丨$\sqrt{(0-\frac{18k}{{k}^{2}+9})^{2}+(1+\frac{9-{k}^{2}}{{k}^{2}+9})^{2}}$=$\frac{18}{9+{k}^{2}}$•$\sqrt{1+{k}^{2}}$,
∴S△BPQ=$\frac{1}{2}$×丨PB丨×丨BQ丨=$\frac{1}{2}$×$\frac{18k}{9{k}^{2}+1}$•$\sqrt{1+{k}^{2}}$×$\frac{18}{9+{k}^{2}}$•$\sqrt{1+{k}^{2}}$,
=$\frac{162k(1+{k}^{2})}{(9+{k}^{2})(1+9{k}^{2})}$,
=$\frac{162(k+{k}^{3})}{9{k}^{4}+82{k}^{2}+9}$=$\frac{162(\frac{1}{k}+k)}{9{k}^{2}+82+\frac{9}{{k}^{2}}}$,
设k+$\frac{1}{k}$=μ,则S△BPQ=$\frac{162μ}{82+9({μ}^{2}-2)}$=$\frac{162}{9μ+\frac{64}{μ}}$≤$\frac{162}{2\sqrt{9μ•\frac{64}{μ}}}$=$\frac{27}{8}$.
当且仅当9μ=$\frac{64}{μ}$即k+$\frac{1}{k}$=μ=$\frac{8}{3}$时取等号,
即(k-$\frac{1}{k}$)2=(k+$\frac{1}{k}$)-4=$\frac{28}{9}$,
k-$\frac{1}{k}$=±$\frac{2\sqrt{7}}{3}$.
直线PQ的斜率k=$\frac{\frac{9{k}^{2}-1}{9{k}^{2}+1}-\frac{9-{k}^{2}}{{k}^{2}+9}}{\frac{18k}{9{k}^{2}+1}+\frac{18k}{{k}^{2}+9}}$=$\frac{{k}^{2}-1}{10k}$=±$\frac{\sqrt{7}}{15}$,
PQ所在的直线方程:y=
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、斜率计算公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.

| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
| A. | (1,4] | B. | [1,4) | C. | [1,4)∪(4,+∞) | D. | (4,+∞) |
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
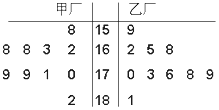 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.