题目内容
11．在△ABC外，分别以AC、BC、AB为边作正方形，得到三个正方形的面积依次为S1、S2、S3，若S1+S2=S3=8，则△ABC的面积最大值是（ ）| A． | 2 | B． | $\sqrt{2}$ | C． | 4 | D． | $\frac{\sqrt{2}}{2}$ |
分析 由题意可得：a2+b2=c2=8，可得C=90°，于是S△ABC=$\frac{1}{2}ab$，再利用基本不等式的性质即可得出．
解答 解：由题意可得：a2+b2=c2=8，
∴C=90°，△ABC是直角三角形，
∴S△ABC=$\frac{1}{2}ab$≤$\frac{1}{2}×\frac{{a}^{2}+{b}^{2}}{2}$=2，当且仅当a=b=2时取等号．
故选：A．
点评 本题考查了勾股定理的逆定理、三角形面积计算公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
口算题天天练系列答案
相关题目
如图，已知⊙C1：（x+$\sqrt{6}$）2+y2=32及点C2（$\sqrt{6}$，0），在⊙C1上任取一点P，连结C2P，作线段C2P的中垂线交直线C1P于点M．
已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的长轴长为4，离心率为$\frac{1}{2}$．
6．定义在区间（0，+∞）上的函数f（x）使不等式2f（x）＜xf′（x）＜3f（x）恒成立，其中f′（x）为f（x）的导数，则（ ）
| A． | 8＜$\frac{f（2）}{f（1）}$＜16 | B． | 4＜$\frac{f（2）}{f（1）}$＜8 | C． | 3＜$\frac{f（2）}{f（1）}$＜4 | D． | 2＜$\frac{f（2）}{f（1）}$＜3 |
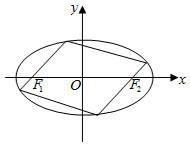已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），其左、右焦点分别为F1（-c，0），F2（c，0）（c＞0）．
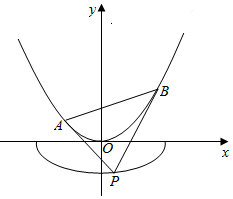如图，已知曲线C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0，y≤0）的离心率e=$\frac{\sqrt{6}}{3}$，且经过点G（1，-$\frac{\sqrt{6}}{3}$），曲线C2：x2=2y，过曲线C1上一点P作C2的两条切线，切点分别为A，B．